1) Для произвольных  , …,
, …, 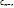 – линейная комбинация:
– линейная комбинация:  =
= 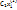 , …,
, …, 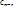
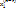 — решение однородной системы ЛАУ (критерий существования ненулевых решений)
— решение однородной системы ЛАУ (критерий существования ненулевых решений)
2)Обратное. Пусть  - произвольное решение системы однородных ЛАУ. Рассмотрим систему решений
- произвольное решение системы однородных ЛАУ. Рассмотрим систему решений 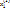 , …,
, …, 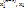 . Она содержит (n-r+1) решений = > является линейно зависимой. Т.е.. существуют такие
. Она содержит (n-r+1) решений = > является линейно зависимой. Т.е.. существуют такие  , …,
, …, 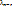 ,
,  (не все равные нулю), что
(не все равные нулю), что 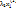 +… +
+… + 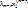 +
+ 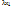 =
=  .
.
Если  = 0, то
= 0, то 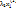 + … +
+ … + 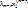 =
=  , причем ∣
, причем ∣  ∣+ … +∣
∣+ … +∣ 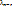 ∣ ≠ 0, чего быть не может = >
∣ ≠ 0, чего быть не может = >
 ≠ 0 и
≠ 0 и  = (
= (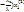 + … + (
+ … + (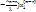 . Обозначим
. Обозначим  = (
= (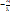 ), i = 1… n-r, таким образом
), i = 1… n-r, таким образом
 =
= 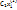 + … +
+ … + 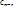
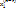 .
.
 2015-04-12
2015-04-12 1571
1571








