Билет 5. Метод Гаусса решения систем ЛАУ

Пусть исходная система выглядит следующим образом

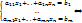
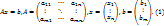
Матрица A называется основной матрицей системы, b — столбцом свободных членов. Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

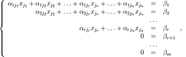
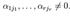
При этом будем считать, что базисный минор основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных x_j1, …, x_jr. Тогда переменные x_j1, …, x_jr называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число β _i ≠0, где i>r, то рассматриваемая система несовместна.

Пусть β _i =0 для любых i>r. Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом x (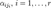, где i — номер строки):

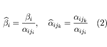, где i=1, …r, k=i+1, …, n. Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

Следствие: Если в совместной системе все переменные главные, то такая система является определённой, а если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной.