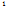Общее решение совместной неоднородной системы линейных алгебраических уравнений

() A = ; () A = ;

Система () называется приведённой однородной системой ЛАУ для неоднородной системы (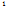). n – число неизвестных, r ≤ n.

Теорема1: общее решение совместной неоднородной системы ЛАУ (1) представляется как сумма некоторого частного решения этой системы и общего решения приведённой системы.

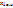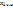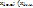= + – некоторое фиксированное решение системы (1); 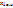– общее решение (1); 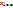– общее решение ())

Доказательство: т.к. (1) совместна, то существует хотя бы одно решение. Фиксируем 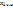, т.е..

A =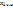

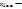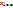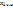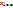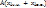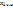1) Пусть произвольное решение (), т.е.. A = . Покажем, что ( + ) – решение (1). Действительно, = A + A 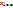= + = > ( 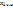+ 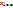) – единственное решение.

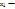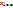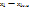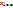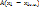2) Пусть произвольное решение (), т.е.. A = . Рассмотрим = . Подставим в (): A = = A — A 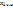= — = ; 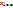– решение ().

= + = +

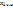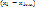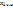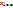
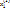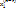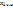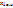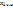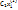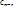
Теорема2: если RgA = Rg = r, причем r < n и , …, – ФСР (1), а — частное решение (1), то = + +… + 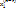, где , …, 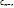– произвольные числа.

(без докозательства)