2015-04-12
2306
V –линейное пространство [e]=(e1…, en) – базис V
[ê]=(ê1, …, ên) — базис V
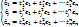êj=(e1, …, en) 
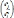j=1,.., n
T=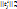 
= 
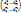(ê1, ê2, … ên)=(e1, e2, …, en) T
[ê]=[e]T T – матрица перехода
Теорема. Если V — n-мерное линейное пространство, то невырожденные
квадратные матрицы порядка n и только они могут являться матрицами
перехода от одного базиса к другому
Док-во: зафиксируем [e]=(e1…, en) – базис V
Необх.: Пусть [ê]=(ê1, …, ên) — другой базис V.По определению матрица перехода T от базиса [e] к базису [ê] состоит из столбцов координат вектора базиса [ê] в базисе [e] т.к. ê1, …, ên – линейно независимы, то столбцы их координат линейно независимы и следовательно, если матрица не вырождена, т.е. если [ê]=[e]T, то det T ≠0.
Дост: Пусть det T≠0 (T- произвольная невыраженная матрица).Построим строку векторов (ê1, ê2, … ên)=(e1, e2, …, en) T.Покажем, что [ê] — базис T=lltjillnn , êk=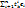 
, k=1, …, n, т.е. в k- ом столбце матрицы T расположен столбец координат êk в базисе [e] т.к. detT ≠0, то столбец T линейно независим по лемме 1 получаем, что вектор ê1, …, ên – линейно независим, Т.к. dim V=n, то ê1, …, ên – образуют базис, т.е. T[e]→ [ê]
|
|
|
Следствие. Если матрица T- матрица перехода от базиса [e] к базису [ê], то матрица перехода от [ê] к базису [e] будет матрица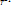 
Док-во: (ê1, ê2, … ên)=(e1, e2, …, en) T. По теореме detT ≠0=> ∃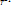
(ê1, ê2, … ên) 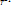=((e1, e2, …, en)T) 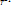=(e1, e2, …, en)T 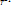=(e1, e2, …, en), т.е.
(ê1, ê2, … ên) 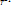=(e1, e2, …, en), где 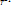–матрица перехода от [ê] к [e]
