Линейно зависимые и линейно независимые системы векторов. Критерий линейной зависимости. Достаточное условие линейной зависимости

Опр. Система элементов x₁,…,x_m лин. пр-ва V наз-ся линейно зависимой, если ∃ λ₁,…, λ_m ∈ ℝ (|λ₁|+…+| λ_m| ≠ 0) такие, что λ₁ x₁ +…+ λ_mx_m = θ.

Опр. Система элементов x₁,…,x_m ∈ V наз-ся линейно независимой, если из равенства λ₁ x₁ +…+ λ_mx_m = θ ⟹λ₁ =…= λ_m =0.

Опр. Элемент x ∈ V наз-ся линейной комбинацией элементов x₁,…,x_m ∈ V, если ∃ λ₁,…, λ_m ∈ ℝ такие, что x= λ₁ x₁ +…+ λ_mx_m.

Теорема (критерий линейной зависимости): Система векторов x₁,…,x_m ∈ V линейно зависима тогда и только тогда, когда хотя бы один вектор системы линейно выражается через остальные.

Док-во. Необходимость: Пусть x₁,…,x_m - линейно зависимы ⟹ ∃ λ₁,…, λ_m ∈ ℝ (|λ₁|+…+| λ_m| ≠ 0) такие, что λ₁ x₁ +…+ λ_m-1x_m-1 + λ_mx_m = θ. Допустим, λ_m ≠ 0, тогда

x_m = (- 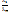) x₁ +…+ (- 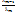) x_m-1.

Достаточность: Пусть хотя бы один из векторов линейно выражается через остальные вектора: x_m = λ₁ x₁ +…+ λ_m-1x_m-1 (λ₁,…, λ_m-1 ∈ ℝ) λ₁ x₁ +…+ λ_m-1x_m-1 +(-1) x_m =0 λ_m =(-1) ≠ 0 ⟹ x₁,…,x_m - линейно независимы.

Дост. условие линейной зависимости:

Если система содержит нулевой элемент или линейно зависимую подсистему, то она линейно зависима.

λ₁ x₁ +…+ λ_mx_m = 0 – линейно зависимая система

1) Пусть x₁ = θ, тогда это равенство справедливо при λ₁ =1 и λ₁ =…= λ_m =0.

2) Пусть λ₁ x₁ +…+ λ_mx_m =0 – линейно зависимая подсистема ⟹|λ₁|+…+| λ_m| ≠ 0. Тогда при λ₁ =0 также получаем, |λ₁|+…+| λ_m| ≠ 0 ⟹ λ₁ x₁ +…+ λ_mx_m =0 – линейно зависимая система.

Базис линейного пространства. Координаты вектора в данном базисе. Координаты сумм векторов и произведения вектора на число. Необходимое и достаточное условие линейной зависимости системы векторов.

Определение: Упорядоченная система элементов e_1, …, e_n линейного пространства V называется базисом этого пространства если:

А) e₁…е_n линейно независимы

Б) ∀ x ∈ α¹… αⁿ такие, что x= α¹ e₁+…+ αⁿ е_n

x= 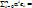α¹e₁+…+ αⁿe_n – разложение элемента x в базисе e_1, …, e_n

α¹… αⁿ ∈ ℝ – координаты элемента x в базисе e_1, …, e_n

Теорема: Если в линейном пространстве V задан базис e_1, …, e_n то ∀ x ∈ V столбец координат x в базисе e_1, …, e_n определяется однозначно (координаты определяются однозначно)

Доказательство: Пусть x=α¹e₁+…+ αⁿe_n и x=β¹e₁+…+βⁿe_n

x= 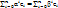⇔ 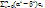= Θ, т. е. e_1, …, e_n — линейно независимы, то - =0 ∀ i=1, …, n ⇔ = ∀ i=1, …, n ч. т. д.

Теорема: пусть e_1, …, e_n — базис линейного пространства V; x, y – произвольные элементы пространства V, λ ∈ ℝ — произвольное число. При сложении x и y их координаты складываются, при умножении x на λ координаты x так же умножаются на λ.

Доказательство: x= 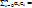(e_1, …, e_n) 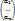и y= 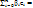(e_1, …, e_n)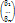

x+y= 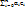+ 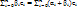= (e_1, …, e_n)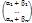

λx= λ 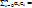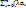) = (e_1, …, e_n)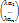

Лемма1: (необходимое и достаточное условие линейной зависимости системы векторов)

Пусть e₁…е_{n —} базис пространства V. Система элементов f₁, …, f_k ∈ V является линейно зависимой тогда и только тогда, когда линейно зависимы столбцы координат этих элементов в базисе e_1, …, e_n

Доказательство: разложим f₁, …, f_k по базису e_1, …, e_n

f_m=(e_1, …, e_n) 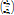m=1, …, k

λ₁f₁+…+λ_kf_k=(e_1, …, e_n)[ λ₁ 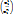+…+ λ_n 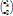] то есть λ₁f₁+…+λ_kf_k= Θ ⇔

⇔ λ₁ 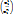+…+ λ_n 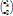= 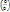что и требовалось доказать.

13. Размерность линейного пространства. Теорема о связи размерности и базиса.
Определение: Линейное пространство V называют n-мерным пространством, если в V существуют n линейно независимых элементов, а система из любых n+1 элементов пространства V линейно зависима. В этом случае n называется размерностью линейного пространства V и обозначается dimV=n.

Линейное пространство называют бесконечномерным, если ∀N ∈ ℕ в пространстве V существует линейно независимая система содержащая N элементов.

Теорема: 1) Если V – n-мерное линейное пространство, то любая упорядоченная система из n линейно независимых элементов этого пространства образует базис. 2)Если в линейном пространстве V существует базис состоящий из n элементов, то размерность V равна n (dimV=n).

Доказательство: 1) Пусть dimV=n ⇒ в V ∃ n линейно независимых элементов e_1,…,e_n. Докажем, что эти элементы образуют базис, то есть докажем что ∀ x ∈ V может быть разложен по e_1,…,e_n. Присоединим к ним x: e_1,…,e_n, x – эта система содержит n+1 вектор а значит она линейно зависима. Поскольку e_1,…,e_n – линейно независима, то по теореме 2 x линейно выражается через e_1,…,e_n т.е. ∃ ,…, такие, что x= α¹ e₁+…+ αⁿ е_n. Итак e_1,…,e_n – базис пространства V. 2)Пусть e_1,…,e_n – базис V, итак в V ∃ n линейно независимых элементов. Возьмем произвольные f₁,…,f_n,f_n+1 ∈ V – n+1 элементов. Покажем их линейную зависимость. Разложим их по базису:

f_m=(e_1,…,e_n) 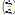= 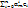где m = 1,…,n Составим матрицу из столбцов координат: A= 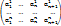Матрица содержит n строк ⇒ RgA≤n. Число столбцов n+1 > n ≥ RgA ⇒ Столбцы матрицы A (т.е. стобцы координат f₁,…,f_n,f_n+1 ) – линейно зависимы. Из леммы 1 ⇒,…,f_n,f_n+1 – линейно зависимы ⇒ dimV=n.

Следствие: Если какой-либо базис содержит n элементов, то и любой другой базис этого пространства содержит n элементов.

Теорема 2: Если система векторов x₁,…,x_m-1, x_m – линейно зависима, а ее подсистема x₁,…,x_m-1 – линейно независима, то x_m - линейно выражается через x₁,…,x_m-1

Доказательство: Т.к. x₁,…,x_m-1, x_m – линейно зависима, то ∃ , …, , ,

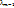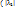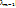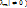, …, | , | такие, что 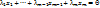. Если 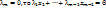, , 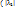…, | 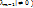=> x₁,…,x_m-1 – линейно независимы, чего быть не может. Значит 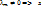_m = (- 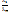) x₁ +…+ (- 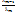) x_m-1.