Теорема о размерности линейной оболочки

V – линейное пространство (|R или |C).

Определение: Пусть 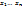- элементы линейного пространства V, а , …, - числа. Рассмотрим линейную комбинацию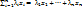

Множество 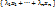всех линейных комбинаций называется

линейной оболочкой системы элементов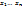

Обозначение: .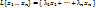

Теорема: Пусть 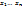- элементы линейного пространства V. Линейная

оболочка 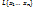является наименьшим линейным подпространством V,

содержащие элементы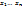

Доказательство: 1) 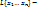линейное подпространство V. Возьмем любые 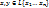. Они имеют следующий вид:

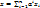
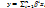для них выполняется:

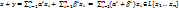
для ∀ 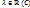выполняется: 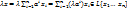=> 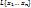- линейное подпространство V.

Пусть L – произвольное линейное подмножество V такое, что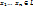

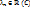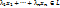∀ , …, : (подпространству) => 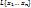наименьшее линейное подпространство, содержащее.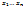

Теорема (о размерности линейной оболочки): Пусть 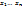- элементы линейного пространства V. Размерность) 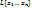линейной оболочки элементов 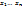равна максимальному числу линейно независимых элементов в системе .

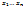Доказательство: Пусть максимальное число линейно независимых элементов в этой системе равно k. Пусть 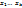- линейно независимы,

тогда элементы 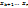через 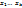линейно выражаются, т.е.
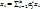(где j = k+1…n).

Покажем, что 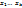- базис ;

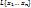а) 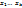- линейно независимы

б)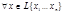

,

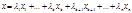
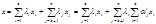т.е. элемент x линейно выражается через 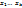=> 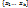– базис линейной оболочки, dim L 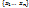=k.