Определение: множество всех векторов x ϵ V таких, что Ax = Θ, называется ядром оператора А.  ker A = {x ϵ V: Ax = Θ }
ker A = {x ϵ V: Ax = Θ }
Определение: множество всех элементов  таких, что
таких, что 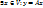 , называется образом оператора А.
, называется образом оператора А.  m A =
m A = 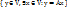
Определение: Линейный оператор пространства V называется обратимым, если существует такой оператор B пространства V, что AB = BA =  , где
, где  – тождественный оператор.
– тождественный оператор.
Оператор В называется обратным к оператору А и обозначается В = А-1.
Свойства обратного оператора:
A ϵ L(Vn):
1° Если А-1 – обратный оператор существует, то он линейный
Доказательство: A А-1 = А-1A = 
а) ∀ x, y ϵ V
А-1(x+y) = А-1(  x+
x+  y) = А-1((A А-1)x + (A А-1)y) = А-1(A(А-1x) + A(А-1y)) = А-1(A(А-1x + А-1y)) =
y) = А-1((A А-1)x + (A А-1)y) = А-1(A(А-1x) + A(А-1y)) = А-1(A(А-1x + А-1y)) = 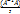 (А-1x + А-1y) = А-1x + А-1y
(А-1x + А-1y) = А-1x + А-1y
б) ∀ λ – число
А-1(λ x) = А-1(λ ∙  x) = А-1(λ (A ∙ А-1)x) = А-1(A(λ А-1x)) =
x) = А-1(λ (A ∙ А-1)x) = А-1(A(λ А-1x)) = 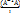 (λ А-1x) = λ А-1x
(λ А-1x) = λ А-1x
Следовательно А-1 – линейный оператор пространства V.
2° Единственность обратного оператора
Доказательство: Пусть AB = BA = 
B = B  I = B(A А-1) = (BA) А-1 =
I = B(A А-1) = (BA) А-1 =  А-1 = А-1
А-1 = А-1
3° Если оператор А обратим, то ядро ker A = {Θ}
Доказательство: Пусть x ϵ ker A, т.е. Ax = Θ 
x =  x = (А-1A)x = А-1(Ax) = А-1(Θ)=Θ
x = (А-1A)x = А-1(Ax) = А-1(Θ)=Θ 
4° Если оператор А обратим, то  m A = V
m A = V
Доказательство: ∀ y ϵ V: y =  y = (A А-1)y = A(
y = (A А-1)y = A(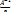 y) ϵ
y) ϵ  m A
m A
Примеры обратимых и необратимых операторов:
1) V2 – пространство геометрических векторов на плоскости
ϕ – фиксированный угол
A=Aϕ – оператор поворота на угол ϕ
Существует А-1=A-ϕ – оператор поворота на угол – ϕ.
Aϕ ∙ A-ϕ = A-ϕ ∙ Aϕ = I ⇒ A – обратим.
2) V3 – пространство геометрических векторов в пространстве.
А – проектированный на плоскость XOI
ker A = 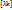 ≠ {Θ} ⇒ A – необратим
≠ {Θ} ⇒ A – необратим
3) ℙn[x] – многочлен степени ≤ n
A= 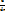 - оператор дифференцирования
- оператор дифференцирования
A(p(x)) = 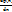 ; A(c) =
; A(c) = 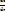 =0 (∀ c ϵ ℝ)
=0 (∀ c ϵ ℝ)
ker A = {ℝ} ≠ {Θ} ⇒ A – необратим.
Теорема (Критерий обратимости линейного оператора):
Пусть A ϵ L(Vn). Оператор А обратим тогда и только тогда, когда он невырожденный, т.е. det A ≠ 0
Доказательство: Vn[e] = (e1, e2, …, en) – фиксированный базис,
[e]: A↔Ae – матрица оператора А в [e] A – обратим ⇔ det A = det Ae ≠ 0
1) Пусть А – обратим, т.е.  А-1 такой, что A ∙ А-1 = А-1 ∙ A =
А-1 такой, что A ∙ А-1 = А-1 ∙ A = 
Обозначим (А-1)e – матрица А-1 в базисе [e], En – матрица  .
.
Известно, что A А-1 = А-1 A =  ⇔ Ae(А-1)e = (А-1)e ∙ Ae = En
⇔ Ae(А-1)e = (А-1)e ∙ Ae = En  матрица Аe – обратима, т.е. det Ae ≠ 0, значит det A = det Ae ≠ 0 и А – невырожден.
матрица Аe – обратима, т.е. det Ae ≠ 0, значит det A = det Ae ≠ 0 и А – невырожден.
Замечание: Матрица (А-1)e и det А-1 = 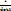
Матрица оператораА-1, обратного оператору А, есть обратная матрица 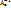 .
.
2) Пусть А – невырожденный оператор, т.е. det A = det Ae ≠ 0.
Следовательно, у матрицы Ae 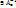 . В [e]: A ↔ Ae; A ϵ L(Vn); Ae ϵ Ln×n
. В [e]: A ↔ Ae; A ϵ L(Vn); Ae ϵ Ln×n
В [e] матрице 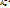 соответствует B ϵ L(Vn). Т.к. Ae
соответствует B ϵ L(Vn). Т.к. Ae 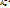 =
= 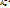 A ⇔ AB = BA =
A ⇔ AB = BA =  ;
;
Значит, В – обратная к А. В силу единственности, B = А-1.
B ↔ Be = 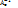 Итак, [e]: A ↔ Ae; и det Ae ≠ 0, то ∃ А-1 ↔
Итак, [e]: A ↔ Ae; и det Ae ≠ 0, то ∃ А-1 ↔ 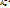 .
.
 2015-04-12
2015-04-12 16316
16316