Билет 27. Критерий диагональности матрицы линейного оператора. Теорема о приведении к диагональному виду матрицы линейного оператора с простыми собственными значениями

Опред. 15. Квадратная матрица A_nxn имеет диагональный вид, если ∀i, j = 1, …, n: i ≠ j, aⁱ_j = 0 (a_ij = 0), т.е.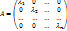

Теорема 11. (Критерий диагональности матрицы линейного оператора в некотором базисе).

Пусть V_n – n-мерное линейное пространство, A Î L(V_n), [e] = (e₁, …, e_n) – базис V_n, A_e – матрица оператора А в [e]. Матрица A_e линейного оператора в базисе [e] диагональна т. и т. т., когда базис состоит из собственных векторов оператора A, причём в этом случае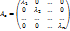

Ae_i = λ_ie_i i=1, …, n (т.е. λ_i собственное значение соответствующее собственному вектору e_i_.)

Док-во: Необходимость. Пусть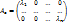

тогда, по определению матрицы линейного оператора, A e₁ = λ₁e₁, …, A e_n = λ_ne_n, т. е. e₁, …, e_n собственные вектора оператора A, отвечающие собственным значениям λ₁, …, λ_n.

Достаточность. Пусть e₁, …, e_n базис из собственных векторов оператора A. Тогда A e_i = λ_ie_i. i = 1, …, n.

[e]: A →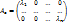

Опред. Оператор называется диагонализируемым, если в пространстве V_n $ базис, в котором матрица оператора диагональна. Оператор диагонализируем в пространстве т. и т. т., когда в V_n $ базис из собственных векторов этого пространства.

Теорема 12. Пусть A Î L(V_n). Если у оператора А $ λ₁, λ₂, …, λ_n - n различных собственных значений, то A – диагонализируемый оператор (т. е. в V_n $ базис, в котором матрица оператора имеет диагональный вид).

Док-во: Собственные значения λ₁, …, λ_n соответствуют системе собственных векторов оператора A: e₁, e₂, …, e_n такая, что A e_i = λ₁e₁, i = 1, …, n. Согласно теореме 10 (Если λ₁, λ₂, …, λ_k– различные собственные значения оператора A (т. е. λ_i ≠ λ_j, при i ≠ j, то собственные вектора f₁, f₂, …, f_k, отвечающие данным собственным значениям являются линейно независимыми)) собственный вектор оператора A, отвечающий различным собственным значениям, линейно независим. Т.к. по условию собственных значений n и λ_i ≠ λ_j при i ≠ j,

то e₁, …, e_n– линейно независим.

Т. к. dim V_n = n, то векторы e₁, …, e_n образуют базис V_n.

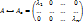
Определение 16. Говорят, что квадратная матрица A приводится к диагональному виду, если она подобна диагональной матрице, т. е. если 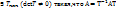, где 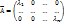– диагональная матрица.