2015-04-12
1414
Теорема: Пусть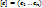 
- некоторый базис пространства 
и В – квадратная матрица порядка n. Тогда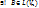 
линейный оператор такой, что матрица В является матрицей оператора В в базисе [e] (т.е. 
).
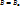Док-во: Построим систему векторов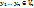 
. 
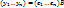
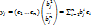j=(1…n)
Согласно лемме 2,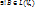 
такой, что 
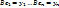[e]:.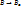 
Найдем 
: 
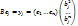Т.е. Ве=В
Вывод: В фиксированном базисе [e] линейного пространства существует
взаимнооднозначное соответствие между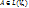 
и матрицей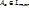 
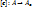
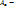матрица A в [e]
Лемма 3: Если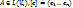 
- базис, 
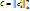- матрица размером nxk, то 
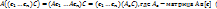без доказательства)
Замечание: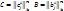 
Если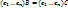 
, то В = С
