1. Расстояние между двумя когерентными источниками d = 0,9 мм. Источники, испускающие монохроматический свет с длиной волны λ = 640 нм, расположены на расстоянии L = 3,5 м от экрана. Определить число светлых полос, располагающихся на 1 см длины экрана.
Дано: d = 9·10-4 м, λ = 640 нм = 64·10-8 м, L = 3,5 м, x = 1·10-2 м.
Найти 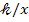
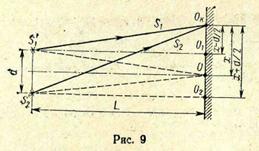
Решение. В точке О на экране (рис. 9) будет максимальная освещенность: точка О равноудалена от обоих источников 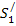 и
и 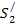 и поэтому разность хода волн
и поэтому разность хода волн 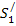 О и
О и 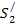 О равна нулю. В произвольной точке экрана
О равна нулю. В произвольной точке экрана 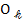 максимум освещенности будет наблюдаться, если оптическая разность хода когерентных волн равна целому числу длин волн:
максимум освещенности будет наблюдаться, если оптическая разность хода когерентных волн равна целому числу длин волн: 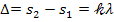 , (1) где
, (1) где 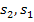 - оптические пути интерферирующих волн; λ — длина волны падающего света;
- оптические пути интерферирующих волн; λ — длина волны падающего света; 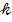 — номер светлой полосы (центральная светлая полоса принята за нулевую).
— номер светлой полосы (центральная светлая полоса принята за нулевую).
Оптическая разность хода волн 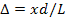 , где
, где 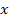 — расстояние
— расстояние
от центральной светлой до -й светлой полосы. Учитывая выражение (1), получим
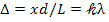 (2)
(2)
Из выражения (2) определяем искомую величину 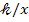 — число светлых интерференционных полос на 1 см длины:
— число светлых интерференционных полос на 1 см длины:
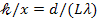 .
.
Подставляя в это выражение числовые значения, получим
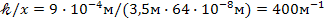 .
.
Ответ: 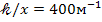 .
.
2. В просветленной оптике для устранения отражения света на поверхность линзы наносится тонкая пленка вещества с показателем преломления 1,26, меньшим, чем у стекла. При какой толщине пленки отражение света от линзы не будет наблюдаться? Длина волны падающего света 0,55 мкм, угол падения 30°.
Дано: λ = 0,55 мкм = 0,55·10-6 м; 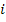 = 30°,
= 30°, 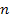 - 1,26.
- 1,26.
Найти 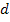 .
.
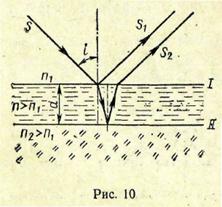
Решение. Свет, падая на систему пленка—стекло под углом i, отражается как от верхней I, так и от нижней II поверхности пленки (рис. 10; n1 < n < п2, n1 и n2 — показатели преломления соответственно воздуха и стекла). Лучи S1 и S2 когерентны, так как образованы из одного луча S. Результат интерференции этих лучей зависит от оптической разности хода. Лучи отражаются от среды с большим показателем преломления, поэтому как на верхней, так и на нижней поверхности пленки происходит потеря полуволны и, следовательно, оптическая разность хода волн равна
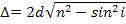 . (1)
. (1)
Условие минимума освещенности при интерференции (условие минимумов) имеет вид
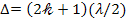 , (2)
, (2)
где 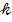 =1, 2, 3,... - порядок интерференционного минимума. Из (1) и (2) следует
=1, 2, 3,... - порядок интерференционного минимума. Из (1) и (2) следует
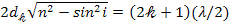 ,
,
откуда
 .
.
Полагая 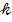 = 1, 2, 3, …, получим ряд возможных значений толщины пленки:
= 1, 2, 3, …, получим ряд возможных значений толщины пленки:
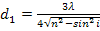 ;
; 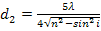 ;
;
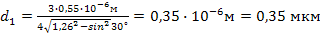 ;
;
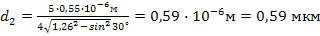 .
.
Ответ; 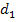 = 0,35 мкм;
= 0,35 мкм; 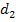 = 0,59 мкм и т. д.
= 0,59 мкм и т. д.
3. На дифракционную решетку Д нормально падает монохроматический свет с длиной волны 0,65 мкм. На экране Э, расположенном параллельно решетке и отстоящем от нее на расстояние 0,5 м, наблюдается дифракционная картина (рис. 11). Расстояние между дифракционными максимумами первого порядка равно 10 см. Определить постоянную дифракционной решетки и общее число глав-
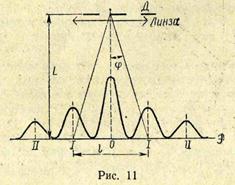
ных максимумов, получаемых с помощью этой решетки.
Дано: λ = 0,65·10-6 м, L = 0,5 м, 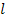 = 0,1 м,
= 0,1 м, 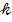 = 1.
= 1.
Найти 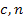 .
.
Решение. Запишем условие главных максимумов дифракционной решетки: 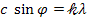 , (1) где с - постоянная дифракционной решетки;
, (1) где с - постоянная дифракционной решетки; 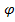 - угол отклонения лучей от нормального направления распространения света;
- угол отклонения лучей от нормального направления распространения света; 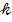 - порядок главного дифракционного максимума; λ — длина волны падающего на решетку монохроматического света.
- порядок главного дифракционного максимума; λ — длина волны падающего на решетку монохроматического света.
По условию задачи, 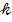 =1. Учитывая, что
=1. Учитывая, что 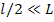 , (см. рис. 11), имеем
, (см. рис. 11), имеем 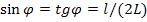 . (2). Подставляя (2) в (1), получим
. (2). Подставляя (2) в (1), получим
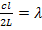 или
или 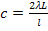 . (3)
. (3)
Подставляя в (3) числовые значения величин, находим
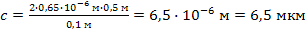 .
.
Для определения общего числа главных максимумов, даваемых дифракционной решеткой, исходим из условия, что максимальный угол отклонения лучей от нормального направления распространения не может превышать 90°, т. е. sin 90°= 1, тогда формула (1) примет вид 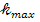 = с/λ. Производим вычисления
= с/λ. Производим вычисления 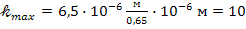 .
.
Общее число максимумов равно 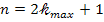 , т. е. влево и вправо от центрального максимума будут наблюдаться по
, т. е. влево и вправо от центрального максимума будут наблюдаться по 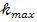 максимумов:
максимумов:
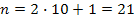
Ответ: с = 6,5·10-6 м, 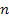 = 21.
= 21.
4. Определить расстояние между атомными плоскостями в кристалле каменной соли, если дифракционный максимум первого порядка наблюдается при падении рентгеновских лучей с длиной волны 0,147 нм под углом 15°12' к поверхности кристалла.
Дано: λ = 0,147 нм = 1,47·10-10 м, 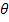 = 15°12',
= 15°12', 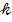 = 1.
= 1.
Найти 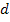 .
.
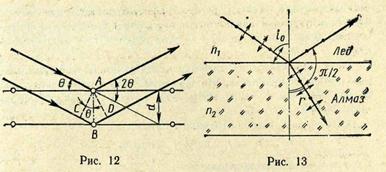
Решение. Дифракция рентгеновских лучей на кристаллах - это результат интерференции рентгеновского излучения, зеркально отражающегося от системы параллельных плоскостей, которые проходят через узлы - атомы (например, А) кристаллической решетки. Эти плоскости называют атомными (рис. 12). Отражение наблюдается лишь в тех направлениях, соответствующих дифракционным максимумам, которым удовлетворяет соотношение
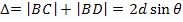 или
или 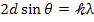 , (1)
, (1)
где 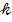 = 1, 2, 3,... - порядок дифракционного максимума;
= 1, 2, 3,... - порядок дифракционного максимума; 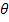 -угол скольжения, т. е. угол между падающим лучом и плоскостью кристалла;
-угол скольжения, т. е. угол между падающим лучом и плоскостью кристалла; 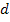 - расстояние между соседними плоскостями, называемое межплоскостным. Исходя из условия (1) и учитывая, что
- расстояние между соседними плоскостями, называемое межплоскостным. Исходя из условия (1) и учитывая, что 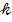 = 1, имеем
= 1, имеем
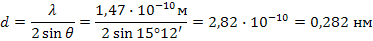
Ответ: 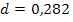 нм.
нм.
5. Луч света, проходя слой льда, падает на алмазную пластинку, частично отражается, частично преломляется. Определить, каким должен быть угол падения, чтобы отраженный луч был максимально поляризован. Найти степень поляризации отраженного и преломленного света для этого угла падения с помощью формул Френеля.
Дано: 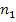 = 1,31,
= 1,31, 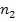 = 2,42.
= 2,42.
Найти: 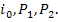
Решение. Отраженный свет максимально поляризован при угле падения 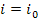 , удовлетворяющем закону Брюстера:
, удовлетворяющем закону Брюстера: 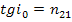 , (1) где
, (1) где 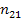 =
= 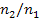 - относительный показатель преломления отражающей среды. Если
- относительный показатель преломления отражающей среды. Если 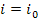 , то отраженный и преломленный лучи взаимно перпендикулярны (рис. 13). Проходящий свет поляризован лишь частично. Из выражения (1) находим
, то отраженный и преломленный лучи взаимно перпендикулярны (рис. 13). Проходящий свет поляризован лишь частично. Из выражения (1) находим
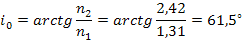
С помощью формул Френеля определяем степень поляризации отраженного луча:
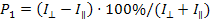
Здесь
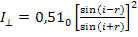 ,
, 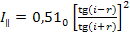
- интенсивности света, распространяющегося в направлениях, перпендикулярном и параллельном плоскости падения; 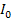 - интенсивность естественного света;
- интенсивность естественного света; 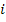 - угол падения;
- угол падения; 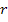 - угол преломления.
- угол преломления.
Если свет падает на диэлектрик под углом полной поляризация (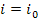 ). то, учитывая, что
). то, учитывая, что 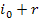 = 90°, для отраженного луча из (2) получим
= 90°, для отраженного луча из (2) получим 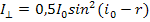 ,
, 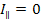 , так как
, так как 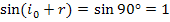 ,
, 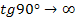
Степень поляризации отраженного луча
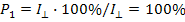
т. е. луч максимально поляризован.
Найдем интенсивности света после преломления в направлениях, перпендикулярном и параллельном плоскости преломления:
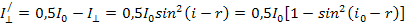 ;
;
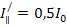 .
.
Степень поляризации преломленного луча
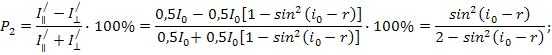
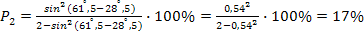 .
.
Ответ: 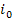 = 61,°5,
= 61,°5, 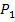 = 100 %,
= 100 %, 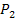 =17 %.
=17 %.
6. Определить, во сколько раз уменьшится интенсивность естественного света, прошедшего через два николя, плоскости поляризации которых составляют угол 45°. Каждый николь поглощает 8 % света, падающего на него (рис. 14).
Дано: α = 45°,  = 0,08.
= 0,08.
Найти 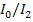 .
.
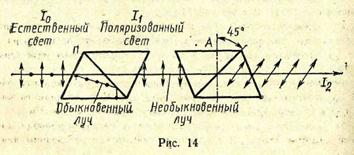
Решение. В результате двойного лучепреломления естественный луч света, попадая в призму П — поляризатор, раздваивается на обыкновенный и необыкновенный лучи. Оба луча поляризованы, но во взаимно перпендикулярных плоскостях. Обыкновенный луч, подчиняясь закону преломления, преломится и, подойдя к слою канадского бальзама в николе, испытывает полное отражение и поглотится зачерненной боковой гранью призмы. Необыкновенный луч проходит через призму без отклонения, интенсивность его уменьшается из-за поглощения света призмой на величину 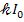 .
.
Интенсивность света, прошедшего через поляризатор, равна 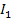 = 0,5(1 —
= 0,5(1 — 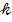 )
) 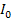 , (1) где:
, (1) где: 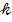 = 0,08 (т.е. 8%) — коэффициент поглощения света в призме;
= 0,08 (т.е. 8%) — коэффициент поглощения света в призме; 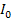 — интенсивность естественного света, падающего на поляризатор.
— интенсивность естественного света, падающего на поляризатор.
Поляризованный свет, войдя во второй николь — анализатор А, опять поглощается и интенсивность его уменьшается на величину 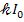 ; кроме того, интенсивность поляризованного света из-за несовпадения плоскостей поляризации поляризатора и анализатора согласно закону Малюса:
; кроме того, интенсивность поляризованного света из-за несовпадения плоскостей поляризации поляризатора и анализатора согласно закону Малюса:
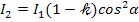 , (2)
, (2)
где α — угол между плоскостями поляризации поляризатора и анализатора; и — коэффициент поглощения; 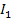 — интенсивность поляризованного света, падающего на анализатор;
— интенсивность поляризованного света, падающего на анализатор; 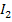 — интенсивность поляризованного света, прошедшего через анализатор. Подставляя выражение (1) в (2), имеем
— интенсивность поляризованного света, прошедшего через анализатор. Подставляя выражение (1) в (2), имеем
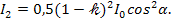 (3)
(3)
Из соотношения (3) следует
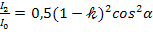 ,
, 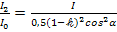 .
.
Подставляя числовые значения, получим
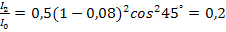 ;
; 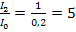 .
.
Ответ: 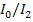 = 5,
= 5,
7. Показатель преломления сероуглерода для света с длинами волн 509, 534 и 589 нм равен соответственно 1,647; 1,640 и 1,630. Вычислить фазовую и групповую скорости света вблизи длины волны 534 нм.
Решение. Групповая скорость 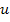 связана с фазовой скоростью
связана с фазовой скоростью 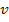 света в среде соотношением
света в среде соотношением
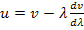 . (1)
. (1)
Учитывая, что 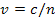 , из (1) получаем
, из (1) получаем 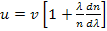 .
.
Для средней дисперсии вещества имеем
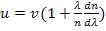 , (2)
, (2)
где 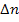 /
/ 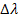 — средняя дисперсия показателя преломления среды. Для λ = 534 нм и
— средняя дисперсия показателя преломления среды. Для λ = 534 нм и 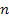 = 1,640 находим относительную дисперсию
= 1,640 находим относительную дисперсию
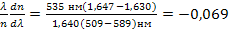 .
.
Из соотношения (2) определяем
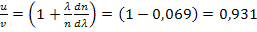 (3)
(3)
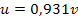 .
.
Учитывая, что фазовая скорость 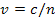 , находим ее значение вблизи λ = 534 нм
, находим ее значение вблизи λ = 534 нм
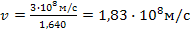 .
.
По формуле (3) вычисляем групповую скорость
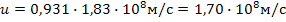
Ответ: 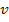 = 1,83·108 м/с,
= 1,83·108 м/с, 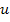 = 1,70·10-8 м/с.
= 1,70·10-8 м/с.
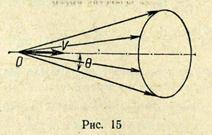
8. В черенковском счетчике из каменной соли релятивистские протоны излучают в фиолетовом участке спектра в конусе с раствором 98°,80; Определить кинетическую энергию протонов. Длина волны фиолетовых лучей 0,4 мкм. Коэффициент преломления для этого участка спектра 1,54.
Дано: λ = 0,4·10-6 м, 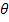 = 49,°40,
= 49,°40, 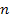 = 1,54,
= 1,54, 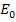 = 938,23 МэВ (см. табл. 18).
= 938,23 МэВ (см. табл. 18).
Найти Ек.
Решение. Если частица движется в веществе со «сверхсветовой» скоростью V, то возникает свечение Вавилова—Черенкова при условии
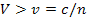 , (1)
, (1)
где 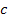 — скорость света в вакууме;
— скорость света в вакууме; 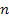 — показатель преломления вещества;
— показатель преломления вещества; 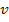 — фазовая скорость света.
— фазовая скорость света.
Свет, возникающий на каждом малом участке траектории заряженной частицы, распространяется вдоль образующих конуса, вершина которого О (рис. 15), расположена на этом участке, ось совпадает с траекторией частицы, а образующие составляют с осью угол
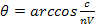 (2) или
(2) или 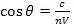 (3)
(3)
Так как излучают релятивистские протоны, то их кинетическая энергия равна
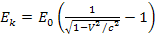 (4)
(4)
Величину V/с определим из соотношения (3)
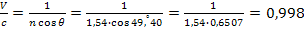 .
.
Используя формулу (4), находим кинетическую энергию
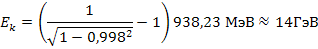
Ответ: 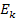 =14 ГэВ.
=14 ГэВ.
9. Во сколько раз увеличится мощность излучения абсолютно черного тела, если максимум энергии излучения передвинется от красной границы видимого спектра к его фиолетовой границе?
Дано: λк = 0,76 мкм; λф = 0,38 мкм.
Найти 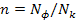 ,
,
Решение. Длина волны, на которую приходится максимум энергии излучения абсолютно черного тела, определяется из первого закона смещения Вина: 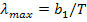 , (1) где Т — термодинамическая температура излучателя;
, (1) где Т — термодинамическая температура излучателя; 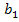 = 2,89·10-3 м·К — постоянная Вина. По формуле (1) определяем температуру, соответствующую красной и фиолетовой границам видимой области спектра:
= 2,89·10-3 м·К — постоянная Вина. По формуле (1) определяем температуру, соответствующую красной и фиолетовой границам видимой области спектра:
Тк = 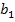 /
/ 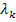 , Тф =
, Тф = 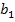 /
/ 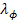
Мощность излучения абсолютно черного тела 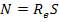 , где
, где 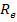 — энергетическая светимость абсолютно черного тела; S — площадь поверхности излучающего тела. В соответствии с законом Стефана—Больцмана
— энергетическая светимость абсолютно черного тела; S — площадь поверхности излучающего тела. В соответствии с законом Стефана—Больцмана
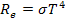 (2)
(2)
где 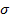 = 5,67·10-8 Вт/(м2·К4) — постоянная Стефана—Больцмана. Для красной и фиолетовой границ видимой области спектра
= 5,67·10-8 Вт/(м2·К4) — постоянная Стефана—Больцмана. Для красной и фиолетовой границ видимой области спектра
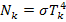 ,
, 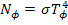
Из формул (1) и (2) следует
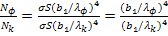 , т.е.
, т.е. 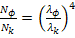
Отношение 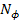 /
/ 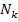 =
= 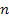 показывает, во сколько раз увеличивается мощность излучения абсолютно черного тела:
показывает, во сколько раз увеличивается мощность излучения абсолютно черного тела:
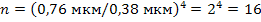
Ответ: Мощность излучения увеличится в 16 раз.
10. На зачерненную поверхность нормально падает монохроматический свет с длиной волны 0,65 мкм, производя давление 0,5·10-5 Па. Определить концентрацию фотонов вблизи поверхности и число фотонов, падающих на площадь 1 м2 в 1 с.
Дано: λ = 0,65·10-6 м, р = 0,5·10-5 Па, 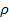 = 0, S = 1 м2,
= 0, S = 1 м2, 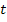 = 1 с.
= 1 с.
Найти: 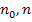 .
.
Решение. Давление света при нормальном падении на поверхность с коэффициентом отражения 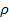 вычисляется по формуле
вычисляется по формуле
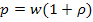 (1) или
(1) или 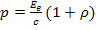 , (2)
, (2)
где 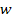 — объемная плотность энергии; Ее — энергетическая освещенность; с — скорость света в вакууме;
— объемная плотность энергии; Ее — энергетическая освещенность; с — скорость света в вакууме; 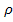 — коэффициент отражения поверхности, в данном случае
— коэффициент отражения поверхности, в данном случае 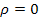 .
.
Объемная плотность энергии равна произведению концентрации фотонов (числа фотонов в единице объема) на энергию одного фотона 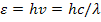 , т.е.
, т.е.
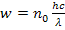 , (3)
, (3)
откуда
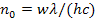 . (4)
. (4)
Определяя объемную плотность энергии из (1) и подставляя в (4), имеем
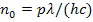 ; (5)
; (5)
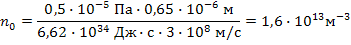
Число фотонов, падающих на площадь 1 м2 за 1 с, численно равно отношению энергетической освещенности к энергии одного фотона:
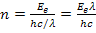 . (6)
. (6)
Энергетическую освещенность определяем из (2) и, подставляя в (6), получаем
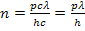 . (7)
. (7)
С учетом (5) выражение (7) примет вид 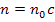 . Подставляя числовые значения, получаем
. Подставляя числовые значения, получаем
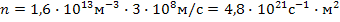
Ответ: 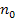 = 1,6·1013 м-3,
= 1,6·1013 м-3, 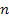 = 4,8·1021с-1·м-2.
= 4,8·1021с-1·м-2.
11. Угол рассеяния фотона с энергией 1,2 МэВ на свободном электроне 60°. Найти длину волны рассеянного фотона, энергию и импульс электрона отдачи. Кинетической энергией электрона до соударения пренебречь.
Дано: ε = 1,2 МэВ = 1,92·10-13 Дж, 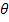 = 60°.
= 60°.
Найти: λ2, Те, ре.
Решение. Изменение длины волны фотона при комптоновском рассеянии равно
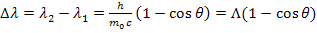 , (1)
, (1)
где 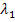 и
и 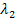 — длины волн падающего и рассеянного фотонов;
— длины волн падающего и рассеянного фотонов; 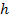 = 6,62·10-34 Дж·с — постоянная Планка;
= 6,62·10-34 Дж·с — постоянная Планка; 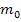 = 9,11·10-31 кг — масса покоя электрона; с = 3·108 м/с — скорость света в вакууме; Λ = 2,43·10-12 м — комптоновская длина волны;
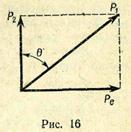
= 9,11·10-31 кг — масса покоя электрона; с = 3·108 м/с — скорость света в вакууме; Λ = 2,43·10-12 м — комптоновская длина волны; 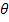 — угол рассеяния (рис. 16). На рисунке
— угол рассеяния (рис. 16). На рисунке 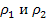 — импульсы падающего и рассеянного фотонов.
— импульсы падающего и рассеянного фотонов.
Из формулы (1) находим 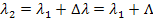 . Выражая
. Выражая 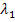 через энергию фотона
через энергию фотона 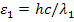 , получаем
, получаем
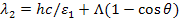 . (2)
. (2)
Энергия электрона, отдачи по закону сохранения энергии равна
Те = 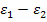 .
.
Выразим изменение длины волны через изменение частоты:
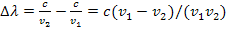 .
.
С учетом (1) можно написать:
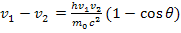 . (3)
. (3)
Умножая выражение (3) на 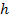 и учитывая, что
и учитывая, что 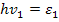 ,
, 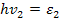 ,
, 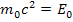 ,
, 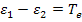 , получаем
, получаем
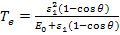 , (4)
, (4)
где 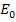 = 0,511 МэВ = 0,82·10-13 Дж — энергия покоя электрона. Зная энергию электрона, найдем
= 0,511 МэВ = 0,82·10-13 Дж — энергия покоя электрона. Зная энергию электрона, найдем
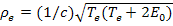 . (5)
. (5)
Подставляя числовые значения в формулы (2), (4) и (5), получаем:
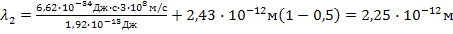 ;
;
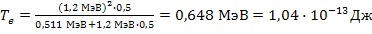 ;
;
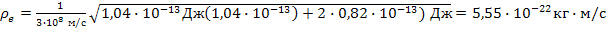 .
.
Ответ: 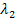 = 2,25·10-12 м;
= 2,25·10-12 м; 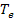 = 0,648 МэВ;
= 0,648 МэВ; 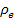 = 5,55·10-22 кг·м/с.
= 5,55·10-22 кг·м/с.
 2015-04-17
2015-04-17 16663
16663
