Отношения между понятиями

Предметы окружающего мира связаны между собой различ­ными отношениями - сходства, тождества, различия. Логика вы­ражает эти взаимосвязи через различные отношения между по­нятиями по содержанию и объему.

------------------------------------- 1 По содержанию отношения между

Отношения между понятиями бывают сравнимыми и
понятиями несравнимыми.

по содержанию Сравнимые — это понятия, в со-

держании которых имеются общие существенные признаки. Например, можно сравнивать понятия «спортсмен» и «студент», «учебный предмет» и «логика», «чувство» и «любовь».

Несравнимыми называются понятия, в содержании которых отсутствуют какие-либо общие признаки. Например, нельзя сравнивать понятия «Закон Божий» и «ЭВМ», «монах» и «стан­ция». Разумеется, любая классификация есть упрощение и в из­вестном смысле относительна. Тем не менее mi пиление нужда-

ется в установлении не только сходства между предметами, но и различия.

В зависимости от того, как соотносятся признаки сравнимых понятий, последние делятся в свою очередь на следующие:

1. Тождественны еили равнозначные, поня­тия (признаки таких понятий полностью совпадают, в языке такие понятия выражаются синонимами, например понятия «первый президент Республики Беларусь» и «А. Г. Лукашенко» тождественны);

2. Сходные, илиоднородные, понятия (у таких по­нятий общей является часть содержания, например, в со­держании понятий «девушка» и «минчанка» есть общие признаки, образующие новое сложное понятие «девушка-минчанка»; «лес» и «парк».

3. Подчиненные понятия (данное отношение возникает тогда, когда признаки одного понятия полностью нахо­дятся в содержании другого понятия, например, в отно­шении подчинения находятся понятия «периодическое издание» и «журнал», «язык программирования» и «Ас­семблер», «офицер» и «подполковник» («подполковник» -это офицер, однако офицер не обязательно подполковник)).

Отношения между понятиями по объему

Поскольку любое понятие имеет не только содержание, но и объем, то любому отношению по содержанию соответствует определенное отно­шение по объему¹:

1. Объемы несравнимых понятий исключают друг друга:

О©

⁴— У V— ' А-понятие «Закон Божий», В-понятие«ЭВМ»;

2. Сравнимые понятия по объему разделяются на совмести­
мые и несовместимые.

Совместимые понятия

Сравнимые совместимые понятия по объему могут:

¹ Для геометрической наглядной иллюстрации отношений между понятиями по объему в логике принято использовать круги Эйлера, Каждому кругу соответ­ствует объем определенного понятия.

2.1.совпадать (такое отношение объемов возникает у тождественных понятий):

А - понятие «А. С. Пушкин»

В - понятие «Автор "Евгения Онегина"»;

2.2. пересекаться (в отношении пересечения находятся понятия, объемы которых частично совпадают):

А — понятие «режиссер» В - понятие «педагоге

2.3.включаться (включение - характеристика отноше­ний между подчиненными понятиями):

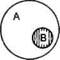А - подчиняющее понятие «офицер»

В - подчиненное понятие «подполковник».

Несовместимые понятия

Сравнимые понятия могут ока­заться и несовместимыми.

Такими понятиями являются:

2.4. контрадикторные (противоречивые) понятия (в отношении логического противо­речия находятся такие понятия, одно из которых утверждает на­личие определенных признаков (А), а другое - отрицает их (не-А), например, понятие А - это «вторник», а понятие не-А - «не­вторник», взятые одновременно, они полностью исчерпывают объем родового понятия):

А - понятие «первый корпус» не-А - понятие «не первый корпус» Круг - объем универсального множества «корпус».

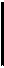Поскольку противоречивые понятия исчерпывают объем универсального множества, к ним применим закон исключенно­го третьего¹;

2.5. контрарные (противоположные, противные) поня­тия (контрарные, или противные, понятия содержат противопо­ложные признаки в пределах одного рода, в предыдущем приме­ре контрарными будут понятия «первый корпус» и «последний корпус», также контрарными будут понятия «белый» - «чер­ный», «любовь» — «ненависть»):

т

А - понятие «белый» В - понятие «черный» С — понятие «красный».

Поскольку противоположные понятия могут не исчерпывать объем родового понятия, то наряду с понятиями А - «белый» и В - «черный» может быть возможно и третье понятие С - «крас­ный». Поэтому к контрарным понятиям закон исключенного третьего не применим². За разными словами русского языка сто­ит разный логический смысл. Понимание логической разницы между противоречием и противоположностью является услови­ем правильного мышления;

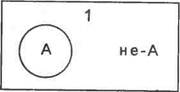
Отношения противоположности и противоречия можно схе­матически показать следующим образом.

©■'©

Противоположные понятия Противоречивые понятия

¹ Так как помимо понятий «А» и «не-А» становится невозможным указать третье

понятие, входящее в данное множество. Характеристика закона исключенного третьего дана в главе 4.

² Помните детскую загадку на понимание: «А, И, Б - сидели на трубе. А - упало,

Б - пропало. Кто остался на трубе?»?

Цифра 1 обозначает объем универсального множества, а само это множество изображено в виде прямоугольника.

Например: 1 - «множество всех ксероксов»; А — «цветной ксерокс»; В - «черно-белый ксерокс», не-А - «нецветной ксе­рокс».

Отношения противоположности и противоречия могут быть изображены на одной схеме.

\_

©'о

не-А

Например: 1 - «множество всех занятий»; А - «полезные за­нятия»; В — «вредные занятия»; не-А — «бесполезные заня­тия».

Поскольку любое понятие имеет как объем, так и содержа­ние, то сопоставление двух и более понятий примет один из представленных в таблице видов сравнимых либо несравнимых понятий;

а) несравнимых по содержанию и исключающих друг друга
по объему;

б) сравнимых по содержанию и совместимых по объему;

в) сравнимых по содержанию и несовместимых по объему.

Если понятия являются тождественными, сходными или под­чиненными по смыслу, то их объемы соответственно совпадают, пересекаются или включаются один в другой. Противоречивые, противоположные и соподчиненные по содержанию понятия об­разуют по объему дополнение, частное исключение или совме­стное включение.

2.6. соподчиненные понятия. Два и более понятий, различных в отдельности, взятые вместе, могут быть совместно подчинены третьему, как виды подчинены роду:

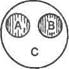А - понятие «липа» В - понятие «дуб» С - понятие «дерево».

Различные отношения между понятиями можно свести в одну таблицу:

Понятия (по содержанию и по объему) жизни

:0©

Сравнимые

Несравнимые: по содержанию - различные по объему исключают друг друга

Совместимые

С	Тождест-	Сходные,	Подчинен-	Контрадик-	Контрар-	Соподчи-
(содер-	венные,	однород-	ные	торные	ные	ненные
жание)	равнознач­ные	ные		(противо­речивые)	(противо­положные)
V (объем)	©	<8В	(ф	d	не-А]	ш	\с/
	Совпаде-	Пересе-	Включение	Дополне-	Частичное	Совмест-
	ние	чение		ние	исключе-	ное вклю-
						ние	чение

Значение понятий

Каково практическое значение изу­чения различных отношений между понятиями? Чрезвычайно велико. Во всех сферах деятельности человек сталкивается с необходимостью употребления понятий, привыч­ных и новых. А поскольку, как мы уже знаем, естественный язык содержит в себе слова-синонимы и слова-омонимы, то отсутст­вие логических навыков в работе с понятиями может обернуться искажением реального положения дел, ложным заключением, нелепым выводом¹ и так далее. «Кто ясно мыслит, тот ясно изла­гает», - гласит известный афоризм. Скудная лексика, непонима­ние слов и идиоматических выражений, ошибочное толкование

пословиц и поговорок¹, неумение правильно выражать в речи родовидовые отношения, различать противоречие и противопо­ложность и другие виды понятий затрудняют образовательный процесс человека и мешают его интеллектуальному развитию.

Подумайте.

Что означают выражения: «понятия не имею», «я без понятия», «это ка­ждый понимает по-своему»?

Значит, главное - научиться точно раскрывать содержание понятия и устанавливать его объем. Это достигается при помощи ряда логических операций с понятиями, о чем и пойдет речь в следующем параграфе, завершающем общую характеристику понятия.