Частные производные функции многих переменных

Пусть функция 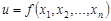определена в окрестности точки 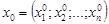. Дадим переменной 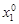приращение 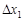, а значения 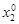, , 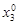, 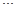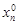оставим без изменения.

Определение 1. Частным приращением функции 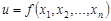по переменной 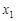в точке 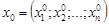называется приращение

.

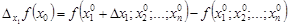Аналогично определяются частные приращения 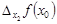, , 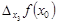, 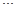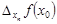по переменным 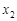, , 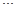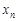в точке .

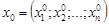Определение 2. Полным приращением функции 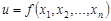в точке 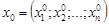называется разность

.

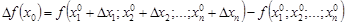Определение 3. Частной производной функции 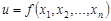по переменной 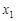в точке 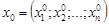называется предел отношения частного приращения функции 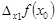к соответствующему приращению аргумента 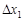, когда 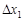произвольным образом стремится к нулю:

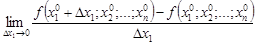. Обозначается: , .

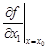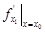Таким образом, имеем:

.

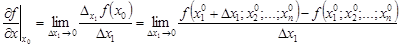Аналогично определяются частные производные 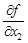, , 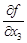, 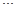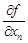по переменным 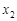, , 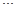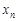в точке .

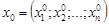Частная производная функции нескольких переменных определяется как производная функции одной из этих переменных при условии, что все остальные переменные остаются постоянными. Вследствие этого, все правила и формулы дифференцирования, справедливые для производных функций одной переменной, имеют место и для частных производных. Однако во всех этих правилах и формулах при нахождении частной производной по какой-либо переменной все остальные переменные считаются постоянными