2015-04-17
35700
Рассмотрим функцию двух переменных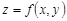 
. Пусть 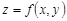определена в окрестности 
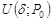точки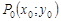 
.
Определение 1. Функция 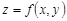называется дифференцируемой в точке 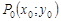, если ее полное приращение в этой точке можно представить в виде
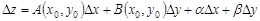, (1)
где 
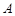и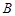 
– некоторые постоянные, зависящие от 
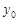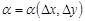и 
; 
и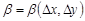 
– бесконечно малые функции от 
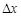и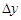 
: 
, 
.
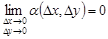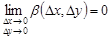Данное равенство выражает условие дифференцируемости функции 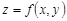в точке .
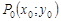Определение 2. Функция 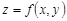, дифференцируемая в каждой точке множества 
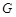, называется дифференцируемой на множестве .
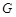Пусть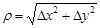 
– расстояние между точкам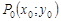и и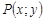 
. Очевидно, что если 
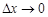и 
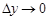, то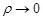 
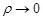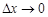, и наоборот, если , то и 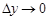, а следовательно, 
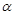и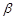 
стремятся к нулю. Тогда сумму 
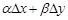можно переписать в виде
,
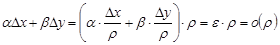так как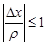 
, 
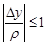и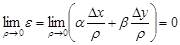 
.
С учетом этого условие дифференцируемости функции в точке 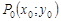можно записать в виде
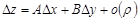, (2)
где 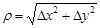– расстояние между точкам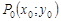и и 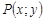, причем 
.
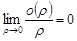Условия дифференцируемости (1) и (2) функции 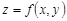в точке 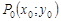эквивалентны.
В равенствах (1) и (2) слагаемое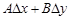 
, линейное относительно 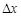и 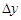, называется главной частью приращения функции, так как оставшееся слагаемое 
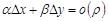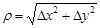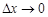является бесконечно малой функцией более высокого порядка малости, чем , при и .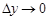
Теорема 1 (связь дифференцируемости и непрерывности). Если функция 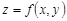дифференцируема в точке 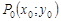, то она и непрерывна в этой точке.
Действительно, по определению функции, дифференцируемой в точке 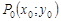, ее приращение представимо в виде
,
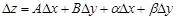где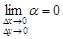 
; 
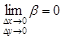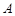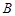; , – некоторые числа, не зависящие от 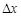и .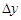
Следовательно,
,
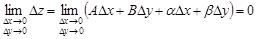а это означает, что функция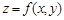 
непрерывна в точке .?
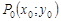Теорема 2 (необходимое условие дифференцируемостифункции нескольких переменных). Если функция 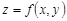дифференцируема в точке 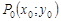, то она имеет в этой точке частные производные 
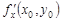и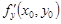 
, причем 
, 
.
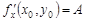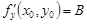Пусть функция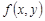 
дифференцируема в точке 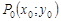, тогда ее приращение представимо в виде (1). Положив в формуле (1) 
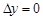, имеем 
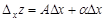. Разделив это равенство на 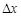и перейдя к пределу при 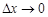, получим
.
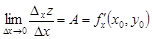Следовательно, в точке 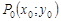существует частная производная 
.
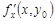Аналогично доказывается существование частной производной 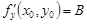в точке .?
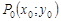Замечание. Утверждения, обратные утверждениям теорем 1 и 2 неверны, т.е. из непрерывности функции, а также существования ее частных производных, еще не следует дифференцируемость функции.
Теорема 3 (достаточное условие дифференцируемости функции нескольких переменных). Если функция 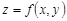имеет частные производные в некоторой окрестности точки 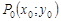, непрерывные в самой этой точке, то она дифференцируема в точке .
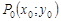Представим полное приращение функции в следующем виде:
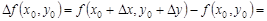
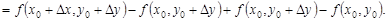
Выражение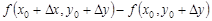 
является приращением функции по переменной 
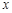. Тогда по теореме Лагранжа
,
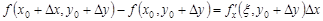где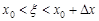 
.
Аналогично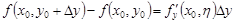 
, где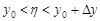 
.
Следовательно,
.
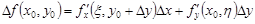По условию теоремы частные производные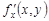 
и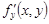 
непрерывны в точке 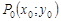. Тогда
, 
.
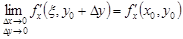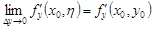Из последних равенств, согласно определению предела, следует, что:
,
,
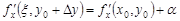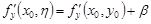где 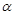, 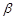– бесконечно малые функции при 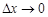, 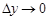. Подставляя выражения для 
, 
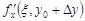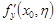в формулу, имеем:
.
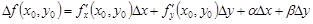Значит, функция 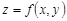дифференцируема в точке .?
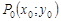Функции с непрерывными частными производными называются непрерывно дифференцируемыми.
Пример. Функция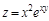 
непрерывно дифференцируема в любой точке 
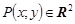, так как ее частные производные 
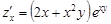и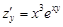 
всюду непрерывны.
Вопрос 3. Определённый интеграл функции на отрезке. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
