Пусть функция 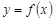 определена и ограничена на отрезке
определена и ограничена на отрезке  ,
, 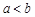 . И пусть
. И пусть 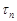 – разбиение отрезка
– разбиение отрезка  на
на 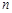 частичных отрезков
частичных отрезков 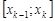 ,
, 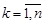 , точками
, точками 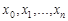 .:
.:
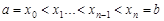 .
.
Тогда 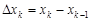 – длина частичного отрезка
– длина частичного отрезка 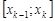 ,
, 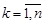 . На каждом таком отрезке произвольным образом выберем точку
. На каждом таком отрезке произвольным образом выберем точку 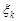 и составим сумму
и составим сумму
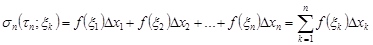 .
.
Определение 2. Сумма
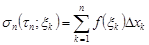 (1)
(1)
называется интегральной суммой Римана для функции  на отрезке
на отрезке  соответствующей данному разбиению
соответствующей данному разбиению 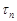 отрезка
отрезка  и выбору промежуточных точек
и выбору промежуточных точек 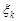 ,
, 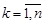 .
.
Пусть 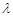 – длина наибольшего частичного отрезка разбиения
– длина наибольшего частичного отрезка разбиения 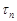 ,
, 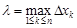 , называемая диаметром разбиения.
, называемая диаметром разбиения.
Определение 3. Функция  называется интегрируемой на отрезке
называется интегрируемой на отрезке  (или интегрируемой по Риману), если существует такое число
(или интегрируемой по Риману), если существует такое число 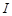 , что для любой последовательности разбиений
, что для любой последовательности разбиений 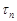 отрезка
отрезка  на частичные отрезки
на частичные отрезки 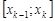 ,
, 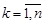 , диаметр которых стремится к нулю при
, диаметр которых стремится к нулю при 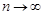 и при любом выборе точек
и при любом выборе точек 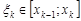 ,
, 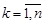 , существует предел интегральных сумм (1) и он равен
, существует предел интегральных сумм (1) и он равен 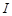 :
:
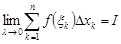 (2)
(2)
Число 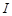 называется определенныминтегралом (или интегралом Римана) от функции
называется определенныминтегралом (или интегралом Римана) от функции  на отрезке
на отрезке  .
.
Обозначается: 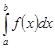 , т.е.
, т.е. 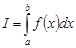 .
.
При этом 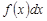 называется подынтегральным выражением,
называется подынтегральным выражением,  – подынтегральной функцией,
– подынтегральной функцией, 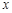 – переменной интегрирования,
– переменной интегрирования, 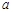 и
и 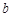 – соответственно нижним и верхним пределами интегрирования.
– соответственно нижним и верхним пределами интегрирования.
Класс всех функций  , интегрируемых по Риману на отрезке
, интегрируемых по Риману на отрезке  , обозначается
, обозначается 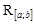 .
.
Определение интеграла Римана на языке 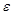 -
- 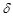 формулируется следующим образом.
формулируется следующим образом.
Определение 4. Число 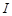 называется определенныминтегралом (или интегралом Римана) от функции
называется определенныминтегралом (или интегралом Римана) от функции  на отрезке
на отрезке  , если для любого
, если для любого 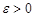 существует такое
существует такое 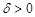 , что каково бы ни было разбиение
, что каково бы ни было разбиение 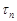 отрезка
отрезка  на частичные отрезки
на частичные отрезки 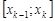 ,
, 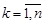 , диаметр которого
, диаметр которого 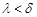 , и каковы бы ни были точки
, и каковы бы ни были точки 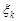 ,
, 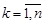 , выполняется неравенство
, выполняется неравенство
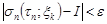 .
.
 2015-04-17
2015-04-17 4732
4732
