Пусть функция 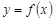 определена в некоторой окрестности точки
определена в некоторой окрестности точки  .
.
Функция 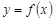 называется дифференцируемой в точке
называется дифференцируемой в точке  , если ее приращение в этой точке
, если ее приращение в этой точке 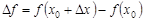 может быть представлено в виде:
может быть представлено в виде:
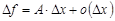 , где
, где 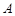 – некоторое действительное число и
– некоторое действительное число и 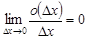 .
.
Для того чтобы функция 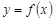 была дифференцируема в точке
была дифференцируема в точке  , необходимо и достаточно, чтобы в точке
, необходимо и достаточно, чтобы в точке  существовала конечная производная
существовала конечная производная 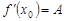 . Если функция
. Если функция 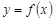 дифференцируема в некоторой точке, то она и непрерывна в этой точке. Если функция
дифференцируема в некоторой точке, то она и непрерывна в этой точке. Если функция 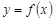 в некоторой точке имеет производную, то она непрерывна в этой точке. Обратное верно не всегда, т. е. из непрерывности функции
в некоторой точке имеет производную, то она непрерывна в этой точке. Обратное верно не всегда, т. е. из непрерывности функции 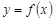 в точке
в точке  еще не следует ее дифференцируемость в этой точке.
еще не следует ее дифференцируемость в этой точке.
Функция  называется дифференцируемой на
называется дифференцируемой на  , если она дифференцируема в любой точке
, если она дифференцируема в любой точке 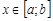 .
.
Дифференциалом функции  называется величина
называется величина 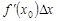 , являющаяся главным (линейным) членом приращения функции в точке
, являющаяся главным (линейным) членом приращения функции в точке  и обозначается
и обозначается 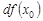 :
:
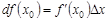 .
.
В частности, если 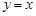 , то
, то 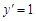 , и, следовательно,
, и, следовательно, 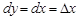 , т. е. дифференциал и приращение независимой переменной равны между собой. Поэтому дифференциал функции
, т. е. дифференциал и приращение независимой переменной равны между собой. Поэтому дифференциал функции  в точке
в точке  можно представить в виде
можно представить в виде
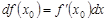 .
.
Тогда приращение функции можно записать в виде 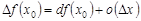 .
.
Видно, что дифференциал функции в точке  отличается от соответствующего приращения функции на бесконечно малую величину более высокого порядка, чем
отличается от соответствующего приращения функции на бесконечно малую величину более высокого порядка, чем 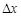 при
при 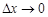 .
.
 2015-04-17
2015-04-17 946
946








