Точка 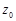 называется изолированной особой точкой функции
называется изолированной особой точкой функции  , если существует окрестность этой точки, в которой
, если существует окрестность этой точки, в которой  аналитична всюду, кроме самой точки
аналитична всюду, кроме самой точки 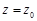 .
.
Изолированная особая точка 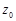 функции
функции  называется:
называется:
– устранимой особой точкой, если существует конечный предел 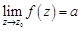 ,
, 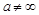 ;
;
– полюсом, если 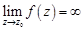 ;
;
– существенно особой, если 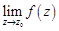 не существует.
не существует.
Точка 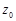 является полюсом порядка
является полюсом порядка 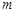 , если для функции
, если для функции 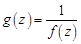 точка
точка 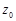 является нулем порядка
является нулем порядка 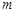 . Полюс порядка
. Полюс порядка 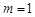 называется простым полюсом.
называется простым полюсом.
Теорема 2 Для того чтобы точка 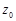 являлась полюсом порядка
являлась полюсом порядка 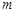 функции
функции  , необходимо и достаточно, чтобы функцию
, необходимо и достаточно, чтобы функцию  можно было представить в виде:
можно было представить в виде:
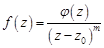 ,где функция
,где функция 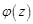 аналитична в точке
аналитична в точке 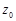 и
и 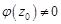 .
.
Аналитическая функция  называется мероморфной в области
называется мероморфной в области 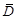
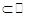 , если
, если  не имеет в ней других особых точек, кроме полюсов.
не имеет в ней других особых точек, кроме полюсов.
Пусть аналитическая функция  в окрестности точки
в окрестности точки 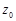 разлагается в ряд Лорана:
разлагается в ряд Лорана:
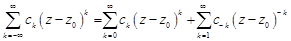 ,
, 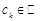 .
.
Теорема 3 Для того чтобы точка 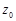 была устранимой особой точкой функции
была устранимой особой точкой функции  , необходимо и достаточно, чтобы ряд Лорана функции
, необходимо и достаточно, чтобы ряд Лорана функции  не содержал членов с отрицательными степенями разности
не содержал членов с отрицательными степенями разности 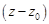 (ряд Лорана не содержит главной части).
(ряд Лорана не содержит главной части).
Теорема 4 Для того чтобы точка 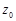 была полюсом функции
была полюсом функции  , необходимо и достаточно, чтобы ряд Лорана функции
, необходимо и достаточно, чтобы ряд Лорана функции  содержал конечное число членов с отрицательными степенями разности
содержал конечное число членов с отрицательными степенями разности 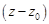 (в главной части ряда содержится конечное число членов).
(в главной части ряда содержится конечное число членов).
Теорема 5 Для того чтобы точка 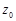 была существенно особой точкой функции
была существенно особой точкой функции  , необходимо и достаточно, чтобы ряд Лорана содержал бесконечно много членов с отрицательными степенями разности
, необходимо и достаточно, чтобы ряд Лорана содержал бесконечно много членов с отрицательными степенями разности 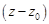 (в главной части ряда содержится бесконечно много членов с отрицательными показателями).
(в главной части ряда содержится бесконечно много членов с отрицательными показателями).
Исследование характера бесконечно удаленной особой точки 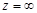 удобнее проводить путем замены
удобнее проводить путем замены 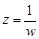 , при которой точка
, при которой точка 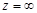 переходит в точку
переходит в точку 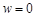 . Тогда:
. Тогда:
– если в разложении в ряд Лорана функции  нет членов с положительными степенями
нет членов с положительными степенями 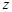 , то бесконечно удаленная точка называется устранимой особой точкой функции
, то бесконечно удаленная точка называется устранимой особой точкой функции  ;
;
– если в разложении в ряд Лорана функции  есть лишь конечное число членов с положительными степенями
есть лишь конечное число членов с положительными степенями 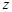 , то бесконечно удаленная точка называется полюсом функции
, то бесконечно удаленная точка называется полюсом функции  ;
;
– если в разложении в ряд Лорана функции  есть бесконечно много членов с положительными степенями
есть бесконечно много членов с положительными степенями 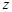 , то бесконечно удаленная точка называется существенно особой точкой функции
, то бесконечно удаленная точка называется существенно особой точкой функции  .
.
Функции 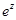 ,
, 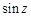 ,
, 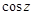 ,
, 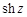 ,
, 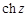 в бесконечно удаленной точке имеют существенную особенность, так как их разложения в ряд Лорана содержат бесконечное множество положительных степеней
в бесконечно удаленной точке имеют существенную особенность, так как их разложения в ряд Лорана содержат бесконечное множество положительных степеней 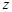 .
.
Вопрос 8 Вычеты и их применение.
 2015-04-17
2015-04-17 801
801








