Вычет 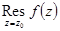 можно найти либо непосредственно по определению
можно найти либо непосредственно по определению
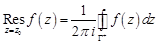 , либо используя разложение в ряд Лорана:
, либо используя разложение в ряд Лорана: 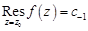 .
.
Рассмотрим вычисление вычетов в различных особых точках.
Вычисление вычетов функции относительно устранимой особой точки. Пусть 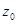 есть устранимая особая точка функции
есть устранимая особая точка функции 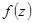 . В этом случае в разложении в ряд Лорана отсутствует главная часть. Поэтому
. В этом случае в разложении в ряд Лорана отсутствует главная часть. Поэтому 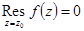 .
.
Вычисление вычетов функции относительно полюса. Пусть точка 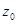 является простым полюсом функции
является простым полюсом функции 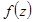 . Тогда вычет находится по формуле
. Тогда вычет находится по формуле
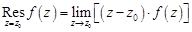 .
.
Если функция 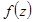 есть частное двух аналитических в точке
есть частное двух аналитических в точке 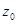 функций
функций 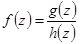 , где
, где 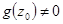 ,
, 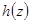 имеет простой нуль в точке
имеет простой нуль в точке 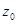 ,
, 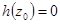 ,
, 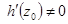 , то точка
, то точка 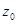 является простым полюсом функции
является простым полюсом функции 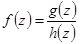 и
и 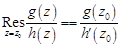 . Пусть точка
. Пусть точка 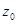 является полюсом порядка
является полюсом порядка 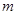 функции
функции 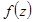 . Тогда вычет находится по формуле
. Тогда вычет находится по формуле
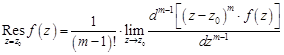 .
.
Вычисление вычетов функции относительно существенно особой точки.Пусть точка 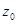 является существенно особой точкой функции
является существенно особой точкой функции 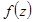 . Тогда для вычисления вычета функции
. Тогда для вычисления вычета функции 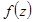 в этой точке непосредственно определяют коэффициент
в этой точке непосредственно определяют коэффициент 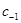 в разложении функции
в разложении функции 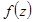 в ряд Лорана.
в ряд Лорана.
Вычет функции 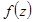 относительно бесконечно удаленной точки
относительно бесконечно удаленной точки 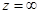 находится с помощью разложения функции
находится с помощью разложения функции 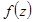 в ряд Лорана в окрестности этой точки. Поэтому вычет функции
в ряд Лорана в окрестности этой точки. Поэтому вычет функции 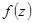 относительно
относительно 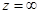 равен взятому с противоположным знаком коэффициенту при первой отрицательной степени в разложении Лорана:
равен взятому с противоположным знаком коэффициенту при первой отрицательной степени в разложении Лорана:
|
|
|
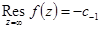 .
.
Вычет аналитической функции относительно бесконечно удаленной устранимой особой точки может оказаться отличным от нуля.
Теорема 1 Если 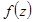 – функция, аналитическая в каждой точке расширенной плоскости
– функция, аналитическая в каждой точке расширенной плоскости 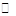 , за исключением конечного числа изолированных особых точек, то
, за исключением конечного числа изолированных особых точек, то
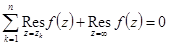 .
.
Вычисление определенных интегралов от функции комплексного переменного.
Вычисление интегралов по замкнутому контуру. Основная теорема о вычетах часто используется для вычисления интегралов комплексного переменного по замкнутому контуру.
Пример. Вычислить 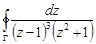 , где
, где
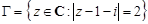 .
.
Решение. В круге 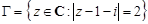 функция
функция 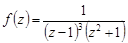 имеет в точке
имеет в точке 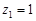 полюс третьего порядка, в точках
полюс третьего порядка, в точках 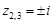 полюсы первого порядка, причем точка
полюсы первого порядка, причем точка 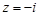 не принадлежит кругу
не принадлежит кругу 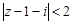 .
.
Тогда
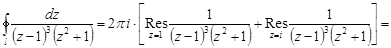
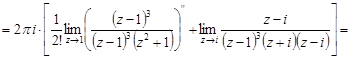
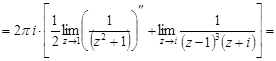
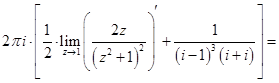
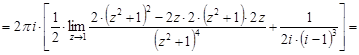
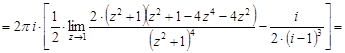
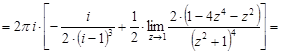
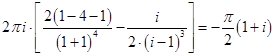 .
.
Вычисление интегралов от рациональных функций. Пусть 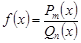 – рациональная функция, где
– рациональная функция, где 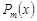 ,
, 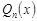 – многочлены степеней
– многочлены степеней 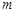 и
и 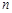 соответственно. Если функция
соответственно. Если функция  непрерывна на всей действительной оси и
непрерывна на всей действительной оси и 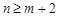 , то
, то
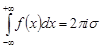 ,
,
где 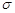 – сумма вычетов функции
– сумма вычетов функции 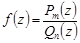 во всех полюсах, расположенных в верхней полуплоскости
во всех полюсах, расположенных в верхней полуплоскости 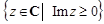 .
.
Пример. Вычислить интеграл 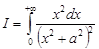 ,
, 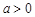 .
.
Решение. Так как подынтегральная функция 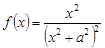 – четная, то
– четная, то
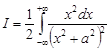 .
.
Введем функцию 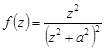 , которая на действительной оси (при
, которая на действительной оси (при 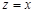 ) совпадает
) совпадает  . Функция
. Функция 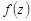 имеет в верхней полуплоскости
имеет в верхней полуплоскости 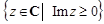 полюс второго порядка в точке
полюс второго порядка в точке 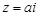 . Вычет
. Вычет 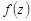 относительно этого полюса равен
относительно этого полюса равен
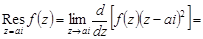
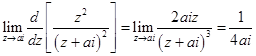 .
.
Тогда 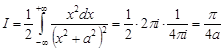 .
.
Интегралы вида 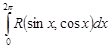 ,где
,где 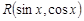 – рациональная функция от
– рациональная функция от 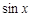 и
и 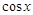 , ограниченная внутри промежутка интегрирования.
, ограниченная внутри промежутка интегрирования.
|
|
|
С помощью замены
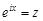 ,
, 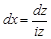 ,
, 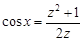 ,
, 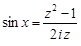
интеграл 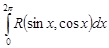 сводится к интегралу от рациональной функции
сводится к интегралу от рациональной функции 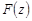 комплексного переменного
комплексного переменного 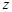 по окружности
по окружности 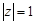 .
.
К интегралу 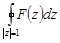 применима основная теорема о вычетах. Тогда
применима основная теорема о вычетах. Тогда 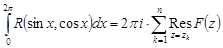 .
.
Пример. Вычислить интеграл 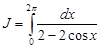 .
.
Решение. Введем замену 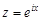 . Тогда
. Тогда
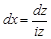 ,
, 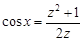 .
.
Подставим в интеграл
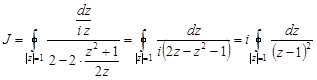 .
.
Функция 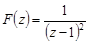 в точке
в точке 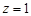 имеет простой полюс 2-го порядка. Поэтому
имеет простой полюс 2-го порядка. Поэтому
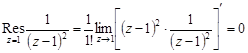 .
.
Отсюда 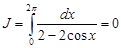 .
.
Интегралы вида 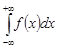 . Вычисление этих интегралов основано на следующей теореме.
. Вычисление этих интегралов основано на следующей теореме.
Теорема 1. Пусть функция  , заданная на всей числовой оси
, заданная на всей числовой оси 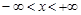 , может быть аналитически продолжена на верхнюю полуплоскость
, может быть аналитически продолжена на верхнюю полуплоскость 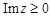 . Функция
. Функция 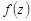 является аналитической в верхней полуплоскости
является аналитической в верхней полуплоскости 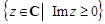 за исключением конечного числа изолированных точек
за исключением конечного числа изолированных точек 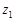 ,
, 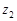 , …,
, …, 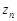 . И пусть существуют такие положительные числа
. И пусть существуют такие положительные числа 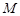 ,
, 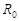 ,
, 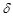 , что для всех точек верхней полуплоскости, удовлетворяющих условию
, что для всех точек верхней полуплоскости, удовлетворяющих условию 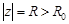 , имеет место оценка
, имеет место оценка 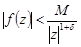 . Тогда несобственный интеграл
. Тогда несобственный интеграл 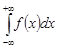 существует и вычисляется по формуле
существует и вычисляется по формуле
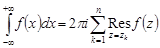 .
.
Пример. Вычислить интеграл 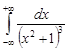 .
.
Решение. Функция 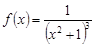 определена на всей действительной оси
определена на всей действительной оси 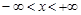 . Ее аналитическое продолжение в верхнюю полуплоскость
. Ее аналитическое продолжение в верхнюю полуплоскость 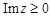 функция
функция 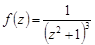 является аналитической в каждой точке верхней полуплоскости за исключением точки
является аналитической в каждой точке верхней полуплоскости за исключением точки 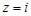 , являющейся полюсом 3-го порядка. На действительной оси полюсов нет При этом для всех точек верхней полуплоскости, удовлетворяющих условию
, являющейся полюсом 3-го порядка. На действительной оси полюсов нет При этом для всех точек верхней полуплоскости, удовлетворяющих условию 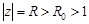 имеет место оценка
имеет место оценка
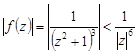 .
.
Поэтому для исходного интеграла можно применить теорему 1
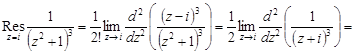
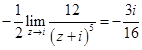 .
.
Следовательно,
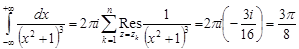 .
.
Интегралы вида 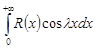 ,
, 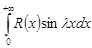 . Интегралы вида
. Интегралы вида 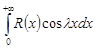 ,
, 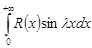 , где
, где 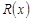 – рациональная функция,
– рациональная функция, 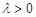 любое действительное число вычисляются с использованием леммы Жордана.
любое действительное число вычисляются с использованием леммы Жордана.
Лемма Жордана. Пусть 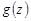 – аналитическая в верхней полуплоскости
– аналитическая в верхней полуплоскости 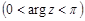 , за исключением конечного числа особых точек, и стремится в этой полуплоскости к нулю при
, за исключением конечного числа особых точек, и стремится в этой полуплоскости к нулю при 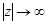 . Тогда при
. Тогда при 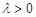
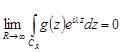 ,
,
где контур 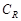 – полуокружность в верхней полуплоскости с центром в точке 0 и радиусом
– полуокружность в верхней полуплоскости с центром в точке 0 и радиусом 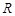 (рис.1.).
(рис.1.).
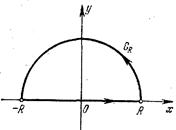
Рис.1.
Пример. Вычислить интеграл 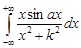 , где
, где 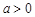 ,
, 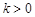 .
.
Решение. Введем вспомогательную функцию
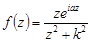 .
.
Видно, если 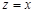 , то
, то 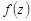 совпадает с подынтегральной функцией
совпадает с подынтегральной функцией 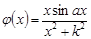 . Рассмотрим контур, указанный на рисунке 1. При достаточно большом
. Рассмотрим контур, указанный на рисунке 1. При достаточно большом 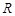 на контуре
на контуре 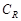 функция
функция 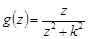 удовлетворяет неравенству
удовлетворяет неравенству 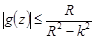 . Следовательно,
. Следовательно, 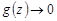 при
при 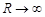 .
.
Значит, по лемме Жордана:
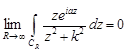 .
.
Для любого 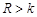 для любого замкнутого контура (рис.1) по теореме о вычетах имеем:
для любого замкнутого контура (рис.1) по теореме о вычетах имеем:
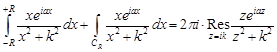 .
.
Вычислим вычет:
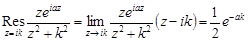 .
.
Тогда
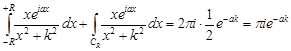 .
.
В пределе при 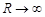 получим
получим
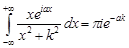 .
.
Учитывая формулу Эйлера:
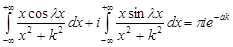
Отделяя слева и справа вещественные и мнимые части, получим
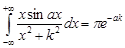 .
.
В силу того, что подынтегральная функция четная, окончательно получим
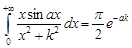 .
.
 2015-04-17
2015-04-17 16692
16692







