Ряд вида 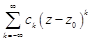 ,называется рядом Лорана. Здесь
,называется рядом Лорана. Здесь 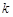
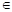
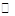 ,
, 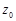 – фиксированная точка комплексной плоскости;
– фиксированная точка комплексной плоскости; 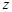 – переменная точка;
– переменная точка; 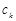
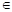
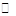 – коэффициенты ряда.
– коэффициенты ряда.
Ряд Лорана представляет собой сумму двух рядов
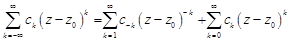 .
.
Ряд 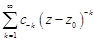 называется главной частью, ряд
называется главной частью, ряд 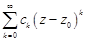 – правильной частью ряда Лорана. Заменой переменной
– правильной частью ряда Лорана. Заменой переменной 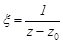 главная часть ряда Лорана преобразуется в степенной ряд, который сходится к аналитической функции
главная часть ряда Лорана преобразуется в степенной ряд, который сходится к аналитической функции 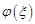 в круге
в круге  . Возвращаясь к переменной
. Возвращаясь к переменной 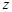 , имеем, что главная часть сходится к функции
, имеем, что главная часть сходится к функции 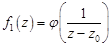 в области
в области 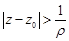 . Область сходимости представляет собой внешность круга радиуса
. Область сходимости представляет собой внешность круга радиуса 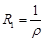 с центром в точке
с центром в точке 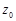 .
.
Правильная часть ряда Лорана представляет собой степенной ряд, поэтому его областью сходимости является круг радиуса 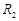 с центром в точке
с центром в точке 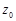 . Внутри этого круга ряд сходится к некоторой аналитической функции
. Внутри этого круга ряд сходится к некоторой аналитической функции 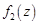 .
.
Если 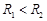 , то существует общая область сходимости рядов, составляющих ряд Лорана. Внутри кольца
, то существует общая область сходимости рядов, составляющих ряд Лорана. Внутри кольца 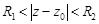 ряд Лорана сходится к некоторой аналитической функции
ряд Лорана сходится к некоторой аналитической функции 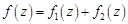 . Если
. Если 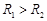 , то ряд Лорана расходится.
, то ряд Лорана расходится.
Областью сходимости ряда Лорана называется общая часть сходимости его главной и правильной частей.
Теорема 2 Функция  , аналитическая в кольце
, аналитическая в кольце 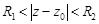 , однозначно представляется в этом кольце рядом Лорана
, однозначно представляется в этом кольце рядом Лорана 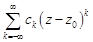 , где коэффициенты
, где коэффициенты 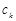 вычисляются по формуле
вычисляются по формуле
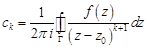 ,
, 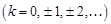 ,
,
 – любой замкнутый контур в кольце
– любой замкнутый контур в кольце 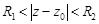 , содержащий точку
, содержащий точку 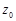 внутри.
внутри.
Рядом Лорана для аналитической функции  в окрестности бесконечно удаленной точки
в окрестности бесконечно удаленной точки 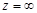 называется ряд
называется ряд 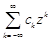 ,сходящийся в кольце
,сходящийся в кольце 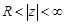 .
.
При преобразовании 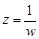 точка
точка 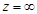 отображается в точку
отображается в точку 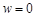 и окрестность бесконечно удаленной точки – в окрестность точки
и окрестность бесконечно удаленной точки – в окрестность точки 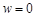 . В окрестности точки
. В окрестности точки 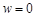 функция
функция 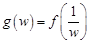 является аналитической и ее разложение в ряд Лорана есть
является аналитической и ее разложение в ряд Лорана есть 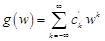 . Возвращаясь к прежней переменной
. Возвращаясь к прежней переменной 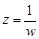 , получаем ряд Лорана для функции
, получаем ряд Лорана для функции  в окрестности бесконечно удаленной точки
в окрестности бесконечно удаленной точки 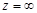 :
: 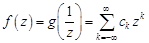 ,где
,где 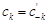 ,
, 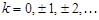 .
.
 2015-04-17
2015-04-17 839
839







