g 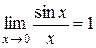 (первый замечательный предел).
(первый замечательный предел).
Предварительно докажем следующее неравенство:
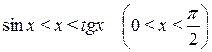 . (4.3)
. (4.3)
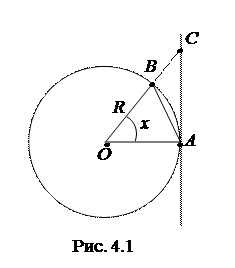
Из рис. 4.1 видно, что при 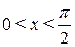 выполнено неравенство:
выполнено неравенство:
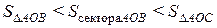 . (4.4)
. (4.4)
Обозначая через x радианную меру угла Ð АОВ, из неравенства (4.4) получим
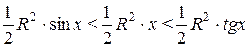 .
.
Далее, после сокращения на 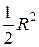 мы приходим к неравенству (4.3).
мы приходим к неравенству (4.3).
Разделив 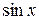 на каждый из членов неравенства (4.3), получим:
на каждый из членов неравенства (4.3), получим:
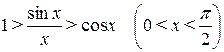 .
.
Следовательно 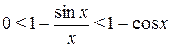 .
.
Но 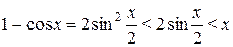 (в силу неравенства 4.3).
(в силу неравенства 4.3).
Таким образом, 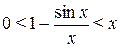 .
.
Из последнего неравенства следует, что
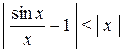 . (4.5)
. (4.5)
В силу нечетности функции 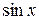 , неравенство (4.5) не изменится при изменении знака x, то есть оно выполнено при всех x ¹ 0,
, неравенство (4.5) не изменится при изменении знака x, то есть оно выполнено при всех x ¹ 0, 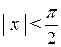 .
.
Неравенство (4.5) позволяет доказать, что 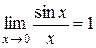 .
.
Действительно, для любого положительного числа e > 0 в качестве d выберем 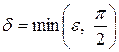 .
.
Тогда при любом x ¹0: 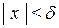 (а, следовательно,
(а, следовательно, 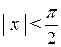 ) будет выполнено неравенство (4.5):
) будет выполнено неравенство (4.5): 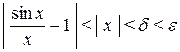 .3
.3
Следствия из первого замечательного предела.
1. g Следствие 1. 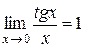 .
.
4 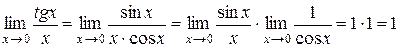 .3
.3
2. g Следствие 2. 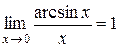 .
.
4 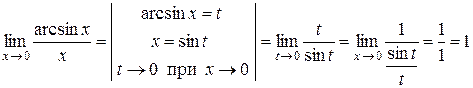 .3
.3
3. 1 Следствие 3. 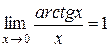 .
.
Следствие 3 доказывается аналогично следствию 2.
Пример 4.7. Найти предел 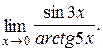
Для раскрытия неопределенности вида 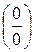 воспользуемся первым замечательным пределом и следствием 3. Для этого разделим числитель и знаменатель дроби на x ¹ 0:
воспользуемся первым замечательным пределом и следствием 3. Для этого разделим числитель и знаменатель дроби на x ¹ 0:
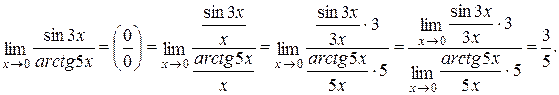
Задача 4.8. Найти предел 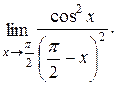
Решение. Мы имеем дело с неопределенностью вида 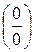 . Произведем
. Произведем
замену переменной: 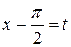 , тогда
, тогда 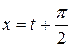 и
и 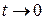 .
.
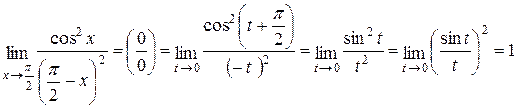 .
.
Сравнение бесконечно малых величин.
Бесконечно малая величина 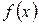 называется бесконечно малой величиной более высокого порядка по сравнению с бесконечно малой величиной
называется бесконечно малой величиной более высокого порядка по сравнению с бесконечно малой величиной 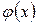 , если
, если 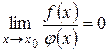 .
.
В этом случае пишут 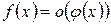 .
.
Две бесконечно малые величины 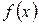 и
и 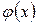 называются бесконечно малыми величинами одного порядка, если
называются бесконечно малыми величинами одного порядка, если 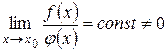 .
.
В данном случае пишут 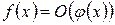 , или
, или 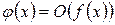 .
.
Две бесконечно малые величины 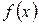 и
и 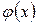 называются эквивалентными бесконечно малыми величинами, если
называются эквивалентными бесконечно малыми величинами, если 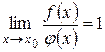 .
.
Первый замечательный предел и его следствия дают нам примеры эквивалентных бесконечно малых величин при 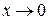 :
:
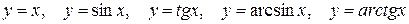 .
.
При решении некоторых задач бесконечно малые величины можно заменять эквивалентными.
Пример 4.9. Найти предел 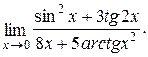
Мы имеем дело с неопределенностью вида 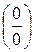 . Заменим бесконечно малую величину
. Заменим бесконечно малую величину 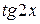 на эквивалентную бесконечно малую величину
на эквивалентную бесконечно малую величину 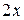 , бесконечно малую величину
, бесконечно малую величину 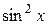 на эквивалентную бесконечно малую величину
на эквивалентную бесконечно малую величину 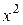 , и бесконечно малую величину
, и бесконечно малую величину 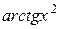 на эквивалентную бесконечно малую величину
на эквивалентную бесконечно малую величину 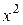 .
.
Получим:
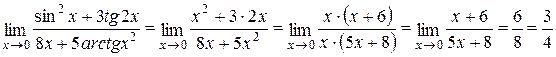 .
.
 2015-04-01
2015-04-01 8996
8996
