Английский математик Брук Тейлор в 1717 году сделал замечательное открытие. Он вывел одну из главных формул математического анализа, имеющую применения в разных областях науки. Тейлор выяснил, что любую дифференцируемую в окрестности некоторой точки функцию с достаточной степенью точности можно заменить многочленом.
Формула Тейлора. Пусть функция  имеет в окрестности точки
имеет в окрестности точки 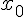 конечные производные до
конечные производные до 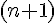 порядка включительно. Тогда для любой точки из этой окрестности имеет место формула:
порядка включительно. Тогда для любой точки из этой окрестности имеет место формула:
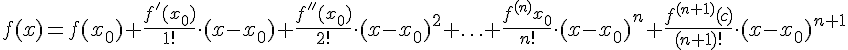
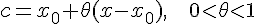 .
.
Эта формула называется формулой Тейлора с остаточным членом в форме Лагранжа. Остаточный член (последнее слагаемое в данной формуле) определяет степень точности, с которой можно заменить функцию соответствующим многочленом.
Формула Тейлора также может быть записана в виде:
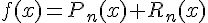 , где
, где
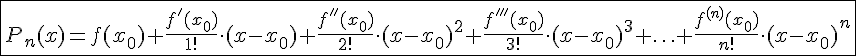 - многочлен Тейлора,
- многочлен Тейлора,
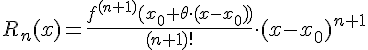 ,
, 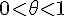 - остаточный член формулы Тейлора, записанный в форме Лагранжа.
- остаточный член формулы Тейлора, записанный в форме Лагранжа. 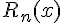 есть погрешность приближенного равенства
есть погрешность приближенного равенства 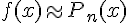 .
.
Остаточный член 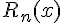 может быть записан в форме Пеано, в этом случае
может быть записан в форме Пеано, в этом случае 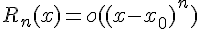 при
при 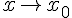 . Такая запись означает, что остаточный член является величиной бесконечно малой более высокого порядка, чем
. Такая запись означает, что остаточный член является величиной бесконечно малой более высокого порядка, чем 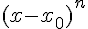 .
.
Иногда многочлен Тейлора 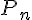 записывают с помощью дифференциалов функции
записывают с помощью дифференциалов функции 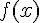 :
:
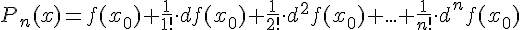
Таким образом, формула Тейлора дает возможность заменить функцию  в окрестности точки
в окрестности точки 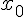 многочленом
многочленом 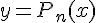 с точностью, равной значению остаточного члена
с точностью, равной значению остаточного члена 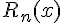 .
.
 2015-07-14
2015-07-14 22682
22682
