2015-04-17
5255
Зиглер и Никольс предложили два метода настройки ПИД-регуляторов [Ziegler]. Один из них основан на параметрах отклика объекта на единичный скачок; второй метод основан на частотных характеристиках объекта управления.
| Табл. 27. Формулы для расчета коэффициентов регулятора по методу Зиглера-Никольса | ||||||
| Расчет по отклику на скачок | Расчет по частотным параметрам | |||||
| Регулятор |  |  |  | |  | |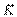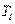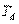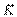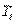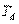
| П |  | - | - |  | - | - |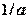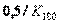
| ПИ |  |  | - |  |  | - |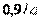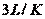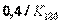
| ПИД |  |  |  |  |  |  |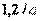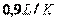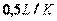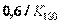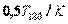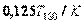
Примечание. Система обозначений параметров регулятора и формулы соответствует уравнению (5.36).
Для расчета параметров ПИД-регулятора по первому методу Зиглера-Никольса используются всего два параметра: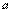 
и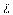 
(см. рис. 5.29 и пояснения к нему в тексте). Формулы для расчета коэффициентов ПИД-регулятора сведены в табл. 27.
 |
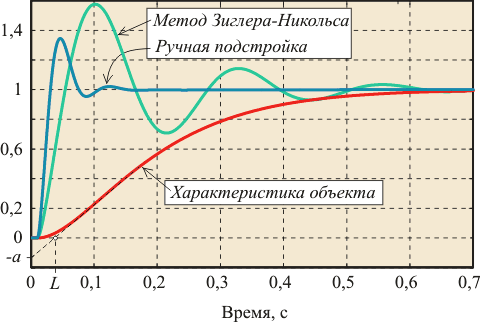Рис. 5.86. Результат настройки ПИД-регулятора по методу Зиглера-Никольса для объекта второго порядка с задержкой:  ,  . |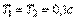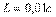
В качестве примера на рис. 5.86 приведен отклик на единичный скачок системы с объектом второго порядка и ПИД-регулятором, настроенным по табл. 27 и переходная характеристика самого объекта управления. Из характеристики объекта получены значения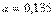 
и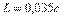 
. По табл.1 для этих значени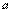й и 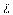можно найти коэффициенты ПИД регулятора: 
, 
, 
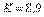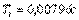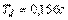. На рис. 5.86 приведен также отклик на единичный скачок той же системы при параметрах 
, 
, 
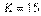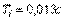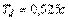, полученных путем ручной подстройки. Как видим, метод Зиглера-Никольса дает параметры, далекие от оптимальных. Это объясняется не только упрощенностью самого метода (он использует только 2 параметра для описания объекта), но и тем, что параметры регулятора в этом методе определялись Зиглером и Никольсом исходя из требования к декременту затухания, равному 4, что и дает медленное затухание процесса колебаний.
Метод Зиглера-Никольса никак не учитывает требования к запасу устойчивости системы, что является вторым его недостатком. Судя по медленному затуханию переходного процесса в системе, этот метод дает слишком малый запас устойчивости.
Второй метод Зиглера-Никольса (частотный метод) в качестве исходных данных для расчета использует частоту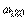 
, на которой сдвиг фаз в разомкнутом контуре достигает 180˚, и модуль коэффициента передачи объекта на этой частоте 
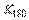. О методике определении этих параметров см. раздел "Частотная идентификация в режиме релейного регулирования". Зная параметр 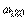, сначала находят период собственных колебаний системы 
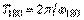, затем по табл.1 определяют параметры регулятора. Точность настройки регулятора и недостатки обоих методов Зиглера-Никольса одинаковы.
