Уравнение прямой на плоскости

Проходящей через две заданные точки

Предположим, что на плоскости заданы две различные точк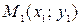и: и 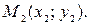В этом случае вектор 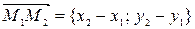будет направляющим вектором единственной прямой, проходящей через две заданные точки, каноническое уравнение такой прямой запишем в виде:

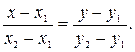
(4)

Общее уравнение прямой на плоскости

Используя свойство пропорции, преобразуем уравнение (4):

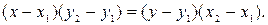
(4а)

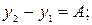
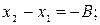
Раскроем скобки и перепишем уравнение (4а), введя следующие обозначения: в результате чего получим:

Утверждение 1. Если в уравнении (5) 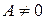или 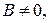то уравнение (5) на плоскости определяет некоторую прямую и называется при этом общим уравнением прямой на плоскости.