Полярными параметрами можно задать положение всякой прямой на плоскости.
 Рис. 4
Рис. 4
| Полярным расстоянием прямой (рис. 4) называется длина p перпендикуляра ОК, опущенного на прямую из начала координат О. Полярное расстояние может быть положительным или равным нулю (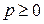 ). Полярным углом прямой называется угол ). Полярным углом прямой называется угол 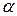 между положительным направлением между положительным направлением
|
оси Ох и перпендикуляром, опущенным на прямую из начала координат. Полярное расстояние и полярный угол называются полярными параметрами прямой. При этом нормальное уравнение прямой можно записать в виде:
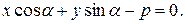
| (10) |
2. ПРЯМЫЕ НА ПЛОСКОСТИ: ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
Утверждение 2. Пусть на плоскости заданы две прямые: 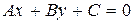 и
и 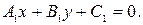 В этом случае выполняется одно и только одно из трех условий:
В этом случае выполняется одно и только одно из трех условий:
1) прямые не имеют общих точек 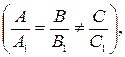 при этом система линейных алгебраических уравнений
при этом система линейных алгебраических уравнений 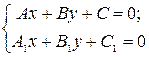 несовместна (имеет пустое множество решений);
несовместна (имеет пустое множество решений);
2) прямые имеют единственную общую точку 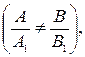 при этом система линейных алгебраических уравнений
при этом система линейных алгебраических уравнений 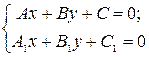 имеет единственное решение
имеет единственное решение 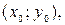 которое может быть найдено, например, по формулам Крамера:
которое может быть найдено, например, по формулам Крамера:
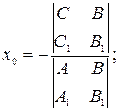
| (11) | 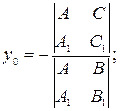
| (12) |
3) прямые совпадают 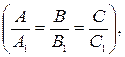 при этом система линейных алгебраических уравнений
при этом система линейных алгебраических уравнений 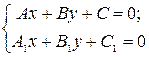 не определена (имеет бесконечно много решений).
не определена (имеет бесконечно много решений).
 2015-04-01
2015-04-01 638
638








