Пусть 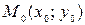 – фиксированная точка плоскости,
– фиксированная точка плоскости, 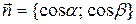 – вектор, заданный своими направляющими косинусами, тогда уравнение вида
– вектор, заданный своими направляющими косинусами, тогда уравнение вида 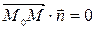 задает прямую на плоскости, проходящую через точку
задает прямую на плоскости, проходящую через точку 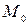 перпендикулярно вектору
перпендикулярно вектору 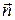 , который называется нормальным вектором этой прямой. Запишем скалярное произведение вектора
, который называется нормальным вектором этой прямой. Запишем скалярное произведение вектора 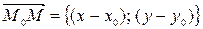 и вектора
и вектора 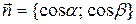 в координатной форме:
в координатной форме:
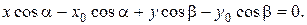
| (8) |
Теперь, введя обозначение 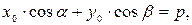 получим нормальное уравнение прямой:
получим нормальное уравнение прямой:
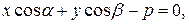
| (9) |
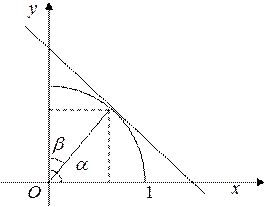 Рис. 3
Рис. 3
| где 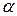 – угол наклона перпендикуляра, опущенного из начала координат на данную прямую, к оси Ох; – угол наклона перпендикуляра, опущенного из начала координат на данную прямую, к оси Ох; 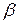 – угол наклона этого перпендикуляра к оси Оу (рис. 3).
Общее уравнение прямой Ax + By + C = 0может быть приведено к нормальному виду при умножении его на нормирующий множитель – угол наклона этого перпендикуляра к оси Оу (рис. 3).
Общее уравнение прямой Ax + By + C = 0может быть приведено к нормальному виду при умножении его на нормирующий множитель 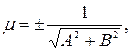
|
взятый со знаком, противоположным знаку свободного члена.
 2015-04-01
2015-04-01 525
525








