Уравнение прямой на плоскости,
Проходящей через данную точку параллельно заданному вектору
Пусть 
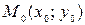 – фиксированная точка плоскости,
– фиксированная точка плоскости, 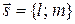 – ненулевой вектор. Тогда уравнение прямой на плоскости, проходящей через точку
– ненулевой вектор. Тогда уравнение прямой на плоскости, проходящей через точку 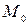 параллельно вектору
параллельно вектору 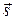 (рис. 1), в векторной форме запишется так:
(рис. 1), в векторной форме запишется так:
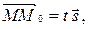 | (1) |
где параметр 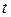 принадлежит множеству действительных чисел; принадлежит множеству действительных чисел; 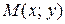 – произвольная точка этой прямой; – произвольная точка этой прямой; 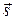 – (в данном случае) направляющий вектор полученной прямой. – (в данном случае) направляющий вектор полученной прямой. | 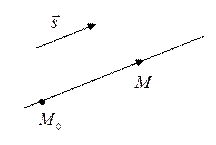 Рис. 1 Рис. 1 |
Параметрические уравнения прямой на плоскости
Перепишем уравнение (1) в координатной форме:
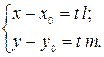 | (1а) |
Выполнив элементарные преобразования, получим параметрические уравнения прямой:
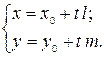 | (2) |
Каноническое уравнение прямой на плоскости
Исключив из системы уравнений (2) параметр t, получим каноническое уравнение прямой на плоскости, проходящей через заданную точку 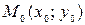 параллельно вектору
параллельно вектору 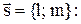
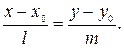 | (3) |
 2015-04-01
2015-04-01 1644
1644