Через одну фиксированную точку 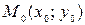 (рис. 6) на плоскости можно провести бесконечное множество прямых. Это множество называется цент-ральным пучком (пучком) прямых, а точка
(рис. 6) на плоскости можно провести бесконечное множество прямых. Это множество называется цент-ральным пучком (пучком) прямых, а точка 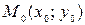 называется центром пучка. Каждую из прямых пучка (кроме той, которая параллельна оси
называется центром пучка. Каждую из прямых пучка (кроме той, которая параллельна оси
ординат) можно представить уравнением:
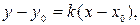
| (17) |
где 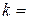 tg tg 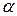 – угловой коэффициент прямой (см. рис. 6).
Уравнение вида (17) называется уравнением пучка прямых с центром в точке – угловой коэффициент прямой (см. рис. 6).
Уравнение вида (17) называется уравнением пучка прямых с центром в точке 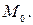
|  Рис. 6
Рис. 6
|
 2015-04-01
2015-04-01 492
492








