Задание 1.Указать особенности в расположении прямых на плоскости (прямая общего положения, проходящая или не проходящая через начало координат; прямая, параллельная оси Ох или Оу): 1) 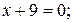 2)
2) 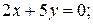 3)
3) 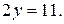 Сделать чертеж каждой прямой в системе координат
Сделать чертеж каждой прямой в системе координат 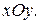
Решение.
1) Уравнение 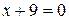 приведем к виду:
приведем к виду: 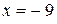 – получили уравнение вида
– получили уравнение вида 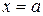 (см. подразд. 1.7, п. б), значит, данная прямая параллельна оси Оу и проходит через точку с координатами
(см. подразд. 1.7, п. б), значит, данная прямая параллельна оси Оу и проходит через точку с координатами 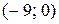 (рис. 8).
(рис. 8).
2) Элементарными преобразованиями уравнение 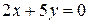 приведем к виду:
приведем к виду: 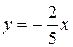 – получили уравнение вида
– получили уравнение вида 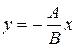 (см. разд. 1.7, п. а), значит, данная прямая проходит через начало координат
(см. разд. 1.7, п. а), значит, данная прямая проходит через начало координат 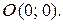 Положив
Положив 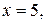 из данного по условию уравнения найдем
из данного по условию уравнения найдем 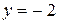 , значит, данная прямая проходит через точку М с координатами
, значит, данная прямая проходит через точку М с координатами 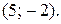 Далее строим прямую, проходящую через точки О и М (рис. 9).
Далее строим прямую, проходящую через точки О и М (рис. 9).
3) Уравнение 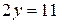 приведем к виду:
приведем к виду: 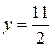 – получили уравнение вида
– получили уравнение вида 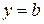 (см. подразд. 1.7, п. в), значит, данная прямая параллельна оси Ох и проходит через точку К с координатами (0; 5,5) (рис. 10).
(см. подразд. 1.7, п. в), значит, данная прямая параллельна оси Ох и проходит через точку К с координатами (0; 5,5) (рис. 10).
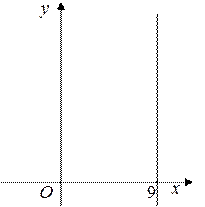 Рис. 8 Рис. 8 |  Рис. 9 Рис. 9 |  Рис. 10 Рис. 10 |
Задание 2.Выбрать из имеющегося списка прямых на плоскости пары: пересекающихся прямых; совпадающих прямых; прямых, не имеющих общих
точек:
1) 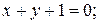 2)
2) 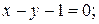 3)
3) 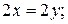 4)
4) 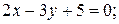 5)
5) 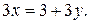
Решение. Для того чтобы применить условия параллельности или пересечения прямых (см. разд. 2, утверждение 2), заданные уравнения перепишем в общем виде. Затем, выписав соотношения между соответствующими коэффициентами, получим:
пересекающиеся прямые: 1 и 2, 1 и 3, 1 и 4, 1 и 5, 2 и 4, 3 и 4, 4 и 5;
совпадающие прямые: 2 и 5;
прямые, не имеющие общих точек, – 2 и 3.
Задание 3.Две точки на плоскости заданы координатами: 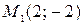 и
и 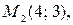
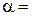 135º – некоторый угол. Составить:
135º – некоторый угол. Составить:
1) уравнение прямой на плоскости, проходящей через точки 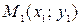 и
и 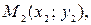 найти ее направляющие косинусы;
найти ее направляющие косинусы;
2) уравнение прямой, проходящей через точку 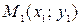 и образующей с осью абсцисс угол
и образующей с осью абсцисс угол 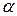 .
.
Решение.
1) Одним из направляющих векторов прямой является вектор 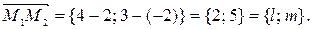 Запишем уравнение прямой в виде:
Запишем уравнение прямой в виде: 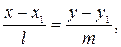 т. е.
т. е. 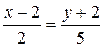 (см. подразд. 1.4). Чтобы записать уравнение в общем виде, воспользуемся свойством пропорции и получим:
(см. подразд. 1.4). Чтобы записать уравнение в общем виде, воспользуемся свойством пропорции и получим: 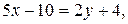 т. е.
т. е. 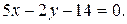 Для того чтобы найти направляющие косинусы прямой, необходимо нормировать ее направляющий вектор. Таким образом, направляющие косинусы могут быть вычислены по формулам:
Для того чтобы найти направляющие косинусы прямой, необходимо нормировать ее направляющий вектор. Таким образом, направляющие косинусы могут быть вычислены по формулам: 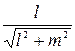 и
и 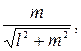 отсюда следует, что косинус угла, образованного данной прямой с положительным направлением оси абсцисс, равен
отсюда следует, что косинус угла, образованного данной прямой с положительным направлением оси абсцисс, равен 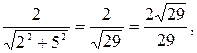 а косинус угла, образованного данной прямой с положительным направлением оси ординат, равен
а косинус угла, образованного данной прямой с положительным направлением оси ординат, равен 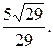
2) Воспользуемся уравнением прямой «с угловым коэффициентом» 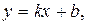 где
где 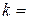 tg
tg 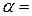 tg 135º
tg 135º 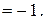 Подставив полученное значение коэффициента k и координаты точки
Подставив полученное значение коэффициента k и координаты точки 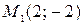 в уравнение
в уравнение 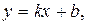 получим:
получим: 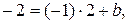 отсюда
отсюда 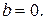 Итак, требуемое уравнение имеет вид:
Итак, требуемое уравнение имеет вид: 
Задание 4.Дано общее уравнение прямой: 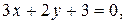 записать для нее следующие виды уравнений:
записать для нее следующие виды уравнений:
1) каноническое 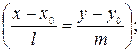
2) параметрические 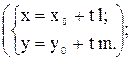
3) «с угловым коэффициентом» 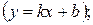
4) «в отрезках» 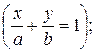
5) нормальное 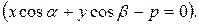
Построить заданную прямую в системе координат хОу.
Решение. Сначала перейдем от общего уравнения прямой к уравнению «с угловым коэффициентом»: 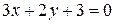 ;
; 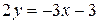 ;
; 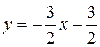 .
.
Используя последнее из уравнений, найдем координаты некоторой точки 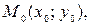 принадлежащей заданной прямой. Положив
принадлежащей заданной прямой. Положив 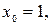 получим:
получим: 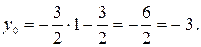 Таким образом, точка
Таким образом, точка 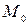 имеет координаты
имеет координаты 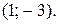 Роль направляющего вектора прямой может играть любой ненулевой вектор, перпендикулярный нормальному вектору данной прямой. Из общего уравнения прямой найдем, что ее нормальный вектор
Роль направляющего вектора прямой может играть любой ненулевой вектор, перпендикулярный нормальному вектору данной прямой. Из общего уравнения прямой найдем, что ее нормальный вектор 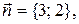 отсюда направляющий вектор
отсюда направляющий вектор 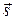 может быть найден из условия:
может быть найден из условия: 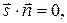 поэтому в качестве направляющего вектора выберем:
поэтому в качестве направляющего вектора выберем: 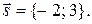 Теперь запишем каноническое уравнение данной прямой:
Теперь запишем каноническое уравнение данной прямой: 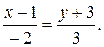
Для записи параметрических уравнений прямой введем параметр: 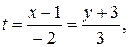 отсюда
отсюда 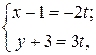 т. е.
т. е. 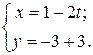
Нормальное уравнение прямой легко получить из общего уравнения, умножив его на соответствующий нормирующий множитель 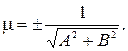 В рассматриваемом случае
В рассматриваемом случае 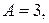
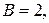
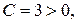 тогда
тогда 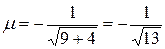 (напомним, что знак при вычислении нормирующего множителя должен быть противоположен знаку свободного члена С общего уравнения прямой). Таким образом, нормальное уравнение прямой имеет вид:
(напомним, что знак при вычислении нормирующего множителя должен быть противоположен знаку свободного члена С общего уравнения прямой). Таким образом, нормальное уравнение прямой имеет вид: 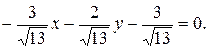
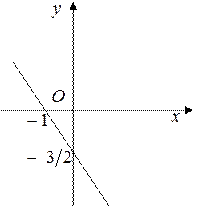 Рис. 11 Рис. 11 | Построение прямой удобнее проводить, если прямая задана уравнением «в отрезках». Для его получения общее уравнение прямой перепишем в виде: 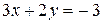 и разделим его на и разделим его на 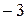 : : 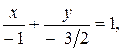 где где 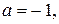 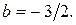 Отсекая на координатных осях соответствующие отрезки, построим данную прямую (рис. 11). Отсекая на координатных осях соответствующие отрезки, построим данную прямую (рис. 11). |
З а д а н и е 5.Даны прямые 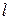
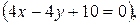
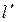
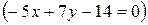 и точка
и точка 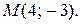 Составить уравнения прямых, проходящих: 1) через точку М параллельно прямой l; 2) через точку М перпендикулярно прямой l. Найти угол
Составить уравнения прямых, проходящих: 1) через точку М параллельно прямой l; 2) через точку М перпендикулярно прямой l. Найти угол 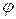 между прямыми
между прямыми 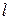 и
и 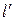 и расстояние d от точки М до прямой l.
и расстояние d от точки М до прямой l.
Решение. Составим уравнение прямой, проходящей через точку М параллельно прямой l. Для этого перейдем от общего уравнения прямой l к ее уравнению «с угловым коэффициентом»: 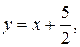 отсюда
отсюда 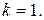 У параллельных прямых угловые коэффициенты равны между собой. Затем из пучка прямых
У параллельных прямых угловые коэффициенты равны между собой. Затем из пучка прямых 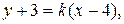 проходящих через точку
проходящих через точку 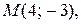 выберем такую, у которой
выберем такую, у которой 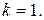 Итак, получим искомое уравнение:
Итак, получим искомое уравнение: 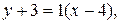 т. е.
т. е. 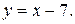
Угловые коэффициенты 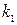 и
и 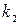 перпендикулярных прямых удовлетворяют соотношению:
перпендикулярных прямых удовлетворяют соотношению: 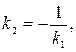 поэтому из пучка прямых
поэтому из пучка прямых 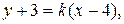 проходящих через точку
проходящих через точку 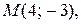 выберем такую, для которой
выберем такую, для которой 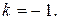 Таким образом, уравнение прямой, проходящей через точку
Таким образом, уравнение прямой, проходящей через точку 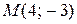 перпендикулярно прямой l, имеет вид:
перпендикулярно прямой l, имеет вид: 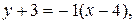 т. е.
т. е. 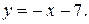
Теперь найдем угол 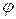 между прямыми
между прямыми 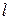 и
и 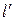 . Запишем уравнение прямой
. Запишем уравнение прямой 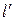 «с угловым коэффициентом»:
«с угловым коэффициентом»: 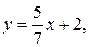 отсюда tg
отсюда tg 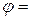
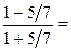
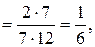
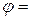 arctg
arctg 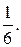 Расстояние d от точки
Расстояние d от точки 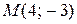 до прямой
до прямой 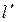 вычислим по формуле:
вычислим по формуле: 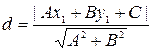 , т. е.
, т. е. 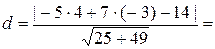
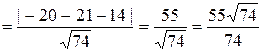 .
.
 2015-04-01
2015-04-01 4121
4121
