Решение. Составим функцию Лагранжа

Составим функцию Лагранжа:

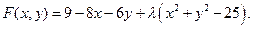
Найдем частные производные первого порядка:

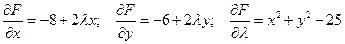
Необходимое условие экстремума функции выражается системой уравнений:

.

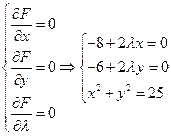Решая эту систему, находим:

.

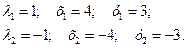Найдем частные производные второго порядка:

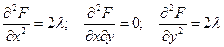
Вопрос о существовании и характере условного экстремума решается на основании исследования знака второго дифференциала:

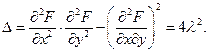
При 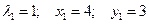, получим

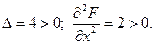
Следовательно, функция имеет в этой точке условный минимум: .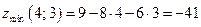

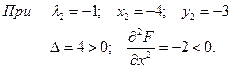
Следовательно, функция в этой точке имеет условный максимум: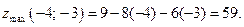

Задание 11. Результаты измерений величин 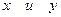приведены в следующей таблице.

Установить зависимость между этими величинами 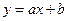методом наименьших квадратов.