Решение. Изобразим область, ограниченную прямыми х = 0; у = 0; х + у = 6

Изобразим область, ограниченную прямыми х = 0; у = 0; х + у = 6:

Найдем частные производные первого порядка:

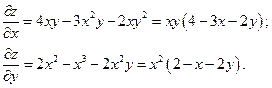
Приравнивая 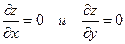, найдем стационарные точки:

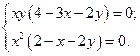
Решение этой системы: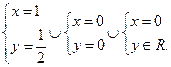

Стационарная точка 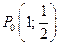лежит внутри треугольника. Значение функции z в этой точке: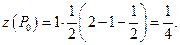

На сторонах треугольника 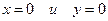значения функции постоянны z = 0.

Найдем ее наибольшее и наименьшее значения на стороне 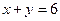. На ней .

.

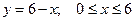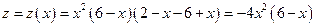На концах интервала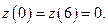

Стационарные точки находим из уравнения:

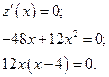
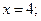
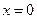- граничная точка.

При х = 4; у = 2;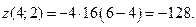

Итак, наибольшее и наименьшее значения функции z в данном треугольнике надо искать среди ее значений:

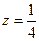- внутри треугольника; в точке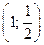

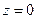- на сторонах 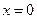и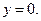

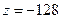- на стороне 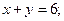в точке (4; 2).

Отсюда получаем, что наибольшее значение 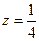данная функция принимает внутри треугольника в точке 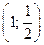; а наименьшее 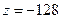- на его границе в точке (4; 2).