Частотные показатели качества

При использовании частотных методов анализа и синтеза систем в качестве типового выходного сигнала берется гармонический сигнал. Использование такого типового сигнала вместо модели реального воздействия на систему связано с простотой математических выкладок, меньшей их трудоемкостью. Гармонический сигнал, являясь лишь отдаленной копией реального воздействия, тем не менее, должен отражать в своих параметрах черты реального воздействия. Это осуществляется введением, так называемого, эквивалентного гармонического сигнала.

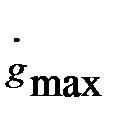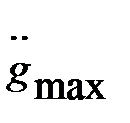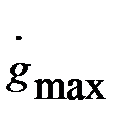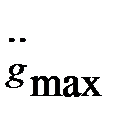Его параметры: амплитуда и частота – находятся на основании таких максимальных наблюдаемых величин реального воздействия, например, задающего g(t), как скорость его изменения и ускорения _. Оценка и может быть получена на основе рассмотрения реального сигнала g(t) или, если такой возможности нет, что случается на начальной стадии проектирования, величинам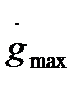и и 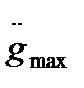приходится задаваться, исходя из каких-либо других соображений, связанных с изучением процессов в объекте регулирования. По мере накопления знаний о системе в процессе проектирования указанные значения могут уточняться.

Важно отметить, что эквивалентное гармоническое воздействие, сформированное подобным образом, представляет собой наиболее «тяжелый» для системы сигнал. Однако, если в процессе проектирования удается рассчитать систему, отвечающую поставленным требованиям при действии на нее такого сигнала, то очевидно, что с менее «тяжелыми» сигналами система «справится».

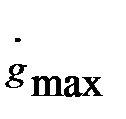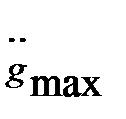Рассмотрим путь формирования эквивалентного гармонического воздействия. Пусть известны максимальные значения и . Выражение для эквивалентного синусоидального сигнала запишем в виде

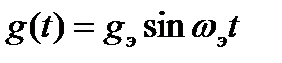(22.46)

Для определения gэ и ωэ, соответствующих 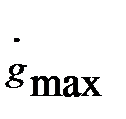и 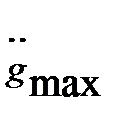, продифференцируем дважды g(t):

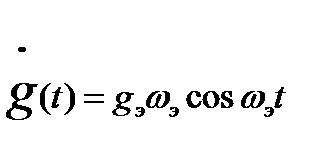(22.47)

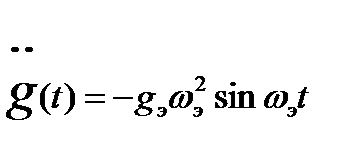(22.48)

Исходя из того, что максимальные значения 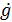(t) и 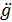(t) равны их амплитудам, запишем:

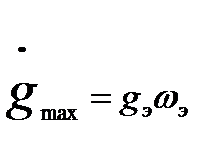(22.49)

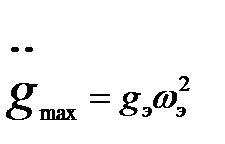(22.50)

Из выражений (22.49) и (22.50) найдем искомые параметры эквивалентного синусоидального воздействия:

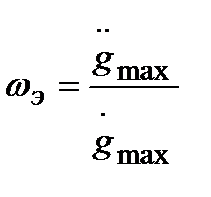(22.51)

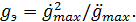(22.52)

Рассмотрим далее оценку точности работы системы. Для этого, воспользовавшись ее передаточной функцией по ошибке, запишем выражение для ошибки x(t) в частотной области. Поскольку в установившемся режиме ошибка также меняется по гармоническому закону, оценим лишь ее максимальное значение x_max, т.е. амплитуду:

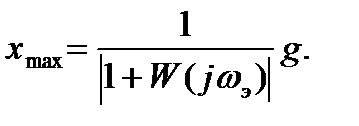
(22.53)

Учитывая, что в установившемся режиме, в диапазоне так называемых рабочих частот системы 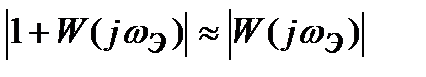, перепишем уравнение (22.4.8):

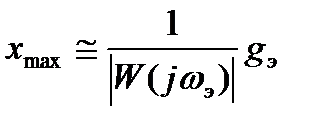. (22.54)

Формула (22.53) позволяет не только определить установившуюся ошибку регулирования при анализе точности системы, но и решить обратную задачу: определить требование к W(jω), выполнение которого будет гарантировать получение ошибки x не более заданной. Это требование можно записать в виде неравенства:

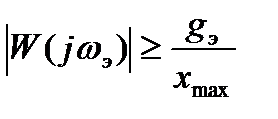
. (22.55)
При использовании для расчетов логарифмических частотных характеристик выражение (22.55) следует переписать в виде:

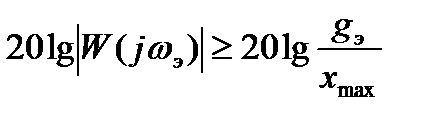
. (22.56)

Графически выполнение требований к точности будет заключаться в прохождении логарифмической амплитудной частотной характеристики L(ω) выше точки A, называемой контрольной точкой, с координатами 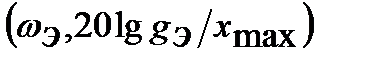как показано на рис. 22.9.

L(ω)

дб

-20дб/дек

A

20lg 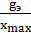-40 дб/дек

ω 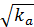k_V ω,с^-1

Рис. 22.9. Построение запретной области для астатических систем

Если рассмотреть случай, когда 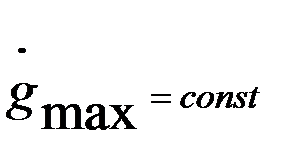, а амплитуда ускорения меньше максимального значения 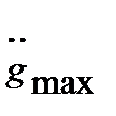, то при различных значениях 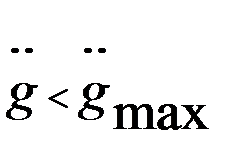в соответствие с (22.51) и (22.52) ω_э будет уменьшаться, а g_э будет увеличиваться. Это графически отобразится в движении контрольной точки А по прямой, имеющей отрицательный наклон
– 20 дБ/дек.

При 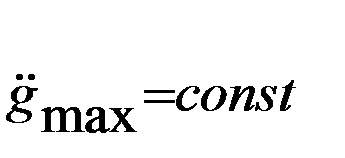и меньших значениях амплитуды скорость ġ, чем
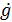_max, эквивалентная частота ω_э будет возрастать, а g_э уменьшаться. Контрольная точка при этом будет двигаться по прямой с наклоном
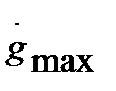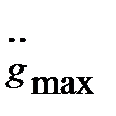– 40 дБ/дек в сторону больших частот. В результате получим так называемую запретную область, обозначенную на рис. 22.9 штриховкой. Для выполнения требований по точности в случае, когда известно максимальные возможные значение и , необходимо, чтобы ЛАХ системы проходила выше запретной области. Иначе говоря, если рассмотреть уравнение (22.53) и получить, что

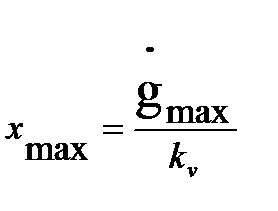(22.57)

и 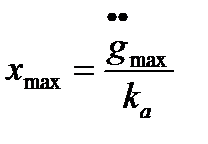, (22.58)

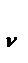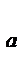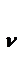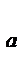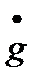
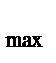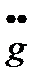
где k и k - соответственно добротность по скорости и ускорению, то выполнение требований по точности для систем с астатизмом 1-го порядка и систем с астатизмом 2-го порядка будет заключаться в необходимости иметь соответственно k и k не меньше значений, рассчитанных по формулам (22.57) и (22.4.58) для максимальных значений , 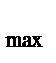и X .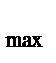

Проделаем аналогичные выкладки для статических систем в случае единичной обратной связи. В данном случае к сведениям о задающем воздействи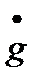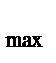и и 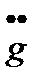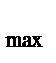необходимо добавить информацию о максимально возможном изменении самого сигнала g 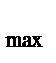. Тогда параметры эквивалентного гармонического воздействия равны:

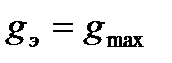(22.59)

ω_э 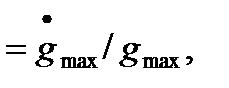(22.60)

а ордината контрольной точки А с учетом уравнения (52) будет:

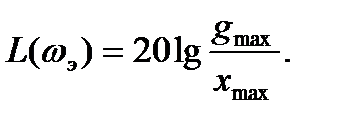(22.61)

При 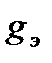= =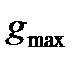const и. 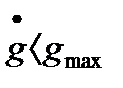контрольная точка перемещается влево по горизонтальной прямой. Пр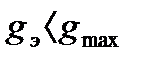и. и 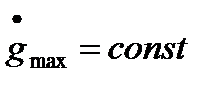увеличивается и точка А перемещается по прямой с наклоном -20дБ/дек. В этом случае
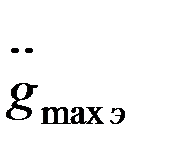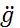˂ _max. Поскольку 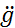_maxэ =ω²g _max..., то предельная частота, до которой движется точка А вправо будет равна

ω_э = 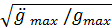(22.62)

На рис. 22.10 показана запретная область для статической системы.

Для того, чтобы ошибка X в установившемся режиме была не больше заданного значения Х_max, ЛАХ системы должен проходить выше данной области.

L(ω)

дб A

20lg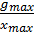

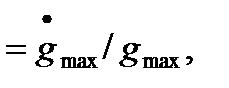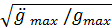ω ω_э = ω,с^-1

Рис. 22.10. Построение запретной области для статической системы

Для учета возмущающих воздействий при формировании запретной области воспользуемся принципом суперпозиции, справедливым для линейных систем. Рассмотрим случай, когда f(t)=f₀1(t). Составляющую ошибки x в формуле (22.16) найдем по формуле

x _устf 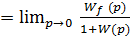, (22.63)

где W_f(p)- передаточная функция разомкнутой системы по возмущению f(t).

Для систем статических по возмущению можно записать:

x _устf = 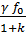, (22.64)

где γ- коэффициент статизма, который может быть определен, например, из статической характеристики объекта регулирования
(рис. 22.11) как тангенс угла α наклона касательной в точке, соответствующей рабочему режиму: γ=. m_x.tgα/m_f, где m_x,m_f- масштабы по оси ординат и абсцисс.

х_{уст f}

0 α f₀

Рис. 22.11. Статистическая характеристика объекта регулирования

Для систем стабилизации, при g(t)=0 обеспечение величины ошибки Х не более требуемого значения Х возможно при условии

1+k ≈ k ≥ f₀g /x _max (22.65)

Запретная зона для данного случая показана на рис. 13 пунктиром. Если же характерным режимом работы является также режим изменения g(t), то запретная область пойдет выше, как показано на рис. 22.13 сплошной линией.

L(ω)

дб A

A_f

20lg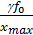

20lg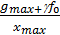

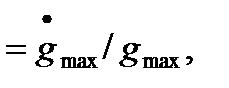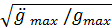ω ω_э = ω,с^-1

Рис. 22.12. Построение запретной области с учетом возмущающего воздействия

Рассмотрим количественные частотные показатели, такого качества систем как запас устойчивости. Как отмечалось, запас устойчивости характеризует удаленность системы от границы устойчивости. Согласно критерию Найквиста нахождению системы на границе устойчивости соответствует прохождение АФЧХ разомкнутой системы через точку с координатами (-1,0) как показано на рис. 22.4.5 а пунктирной линией.

а б

jV

jV U₂=b₂

U₁= 1/b₁

-1,j0

-1,j0 U * U

j_з 0 2 1

R=1

j W(jw)

W(jw)

Рис. 22.13. Определение запаса устойчивости по АФЧХ

Для того чтобы определить удаленность системы, АФЧХ которой показана на рис. 22.13 а и б сплошной линией, от границы устойчивости, вводятся такие количественные показатели как запас устойчивости по фазе и запас устойчивости по модулю.

Запасом устойчивости по фазе. j_з называется угол

j_з = 180 + j (22. 66)

где.. j - аргумент (отрицательный) частотной передаточной функции разомкнутой системы W(jw) при 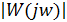=1 (рис. 22.13,а). Из практики известно, что для большинства систем... j_з =30÷60⁰.

Запас устойчивости по модулю является количественной мерой удаленности точек 1 и 2 (ри22.13,б, случай условно-устойчивой системы) от точки с координатами (-1,0) и выражается в децибелах:

L₁ = 20 lg b₁ = 20 lg 1/U₁ (22.67)

L₂ = 20 lg b₂ = 20 lg U₂ (22.68)

Как показала практика, для работающих систем запас устойчивости по модулю лежит в пределах 6+20 дБ.

Оценка запаса устойчивости требует одновременного определения запасов устойчивости по фазе и по модулю. Наличие двух количесвенных показателей является определенным недостатком. В этом отношении удобнее использовать лишь один количественный показатель запаса устойчивости -показатель колебательности М, который представляет собой максимум модуля частотной передаточной функции замкнутой системы (рис.22.14) при начальной ординате, равной единице, т.е. 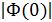=1:

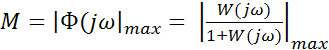(22.69)

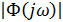
М

0 ω, 1/с

ω_р

Рис. 22.14. Амплитудные частотные характеристики замкнутой системы

Наличие максимума характеристики |Ф(jω)| объясняется резонансными свойствами системы. Чем больше по величине резонансный пик при частоте резонанса ω_р, тем больше склонность системы к колебаниям, тем больше перерегулирование σ в переходных процессах и тем меньше запас устойчивости.

При анализе и синтезе систем, учитывая взаимно-однозначное соответствие между Ф(jw) и W(jw), большую часть исследований проводят, оперируя с W(jw), делая затем заключения о свойствах замкнутой системы (вспомните, например, критерий Найквиста). Объясняется это простотой выражения W(jw) по сравнению с Ф(jw), за счет чего достигается меньшая трудоемкость расчетов.

Рассмотрим в данном случае возможность определять показатель колебательности М по частотной передаточной функции разомкнутой системы W(jw).

Для этого представим выражение (22.69) в виде:

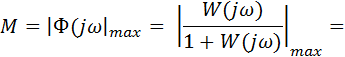
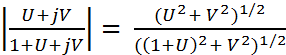(22.70)

где W(jw)=U+jV, а U и V-соответственно вещественная и мнимая части W(jω).

Возведем левую и правую части уравнения (22.70) в квадрат и преобразуя полученное выражение получим:

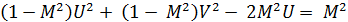(22.71)

Разделив уравнение (70) на (1- 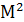) и добавив к его левой и правой частям слагаемое 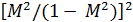....., будем иметь:

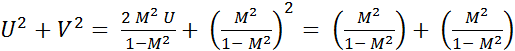(22.72)

Преобразуя (22.72) получим:

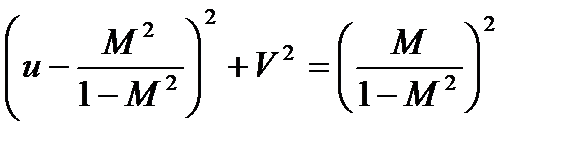(22.73)

Выражение (22.73) представляет собой уравнение окружности на комплексной плоскости с центром в точке с координатами

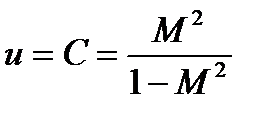, V = 0 (22.74)

и с радиусом 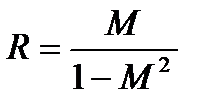. (22.75)

В хорошо демпфированных системах показатель колебательности M обычно не превосходит значений 1,1 + 1,5, хотя может иметь в некоторых случаях и значения 2 + 2,5. Точность определения M не выше 0,05.

В соответствии с выражениями (22.74) и (22.75) на рис. 22.4.7, а показаны окружности для нескольких значений M (для M₁ C = C₁, R = R₁).

а б

C₁ jV jV

M₁

-1, j0

-1, j0

M₂ 0 U M₁ M ₂ 0 U

R₁

M₃

W(jω)

M₁ ˂ M₂ ˂ M₃

Рис.. 22.15. К вопросу определения запаса устойчивости с помощью показателя колебательности M

Из проделанных рассуждений следует, что окружность для определенного значения M на комплексной плоскости (рис.22.15, а, б) является отображением прямой 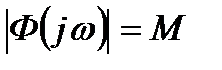на графике 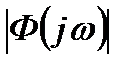как функции ω (рис. 22.14).

Для определения показателя колебательности системы на комплексной плоскости строятся окружности для различных значений M. Затем строится АФЧХ разомкнутой системы и определяется, какой из окружностей она касается. На основании этого делается заключение о величине M.

При проектировании систем требования к запасу устойчивости систем могут ставиться в виде максимально допустимого показателя колебательности 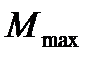. Данные требования считаются выполненными тогда, когда АФЧХ разомкнутой системы не заходит в так называемую запретную область, ограниченную окружностью, построенной для данного показателя. На рис. 22.16,а запретная область заштрихована.

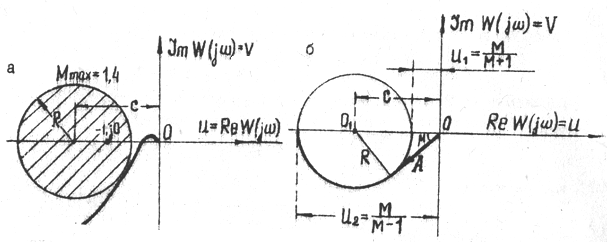
Рис. 22.16. Запретная область для АФЧХ.

Поскольку одной из удобных форм графического представления частотных характеристик являются логарифмические частотные характеристики (ЛЧХ), рассмотрим построение запретной области в этом случае. Предварительно получим так называемые μ – кривые, представляющие собой зависимость величины 20 lgA в децибелах, где A вектор, конец которого лежит на нижней полуокружности для рассматриваемого показателя M, от величины угла μ (см. рис. 22.16,б) следует, что

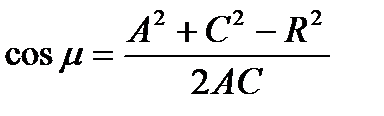. (22.76)

Так как

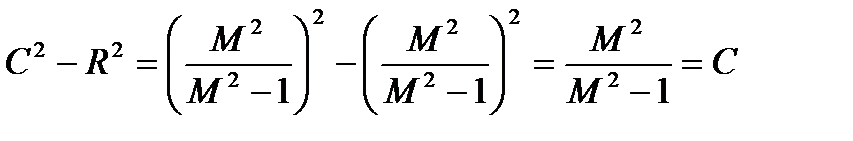, (22.77)

то уравнение (22.4.30) можно переписать в виде

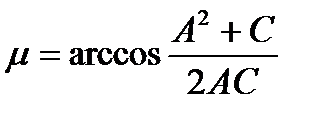. (22.78)

Задаваясь различными значениями A от 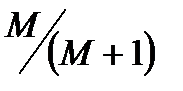до 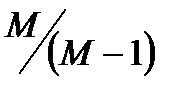при C=const и M=const, можно получить значения μ и 20 lgA построить так называемые μ – кривые, показанные на рис. 22.17.

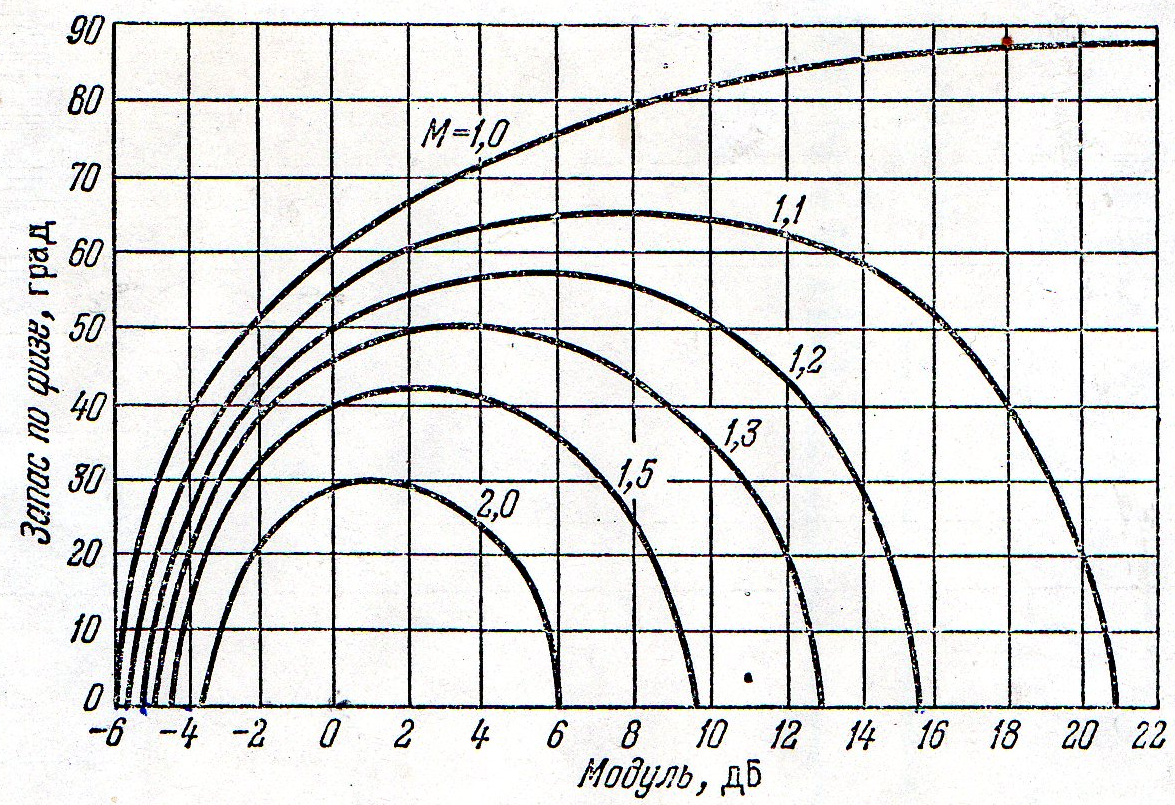
Рис. 22.17. – Кривые для различных значений М

Определение того, удовлетворяет ли система требуемому показателю колебательности, осуществляется следующим образом. Строится ЛЧХ системы (рис22.18,б).

Затем в тех же масштабах, что и ЛАХ и ЛФХ строится μ – кривая (рис. 22.18,б кривая). Далее величина μ для различных значений 20 lgA откладывается от оси абсцисс для тех же значений ЛАХ системы 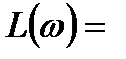20 lgA. Ход построения запретной области показан с помощью стрелок на рис. 22.18, б. На рис. 22.18,а тот же случай, что и на рис. 22.18,б представлен на комплексной плоскости для АФЧХ системы.

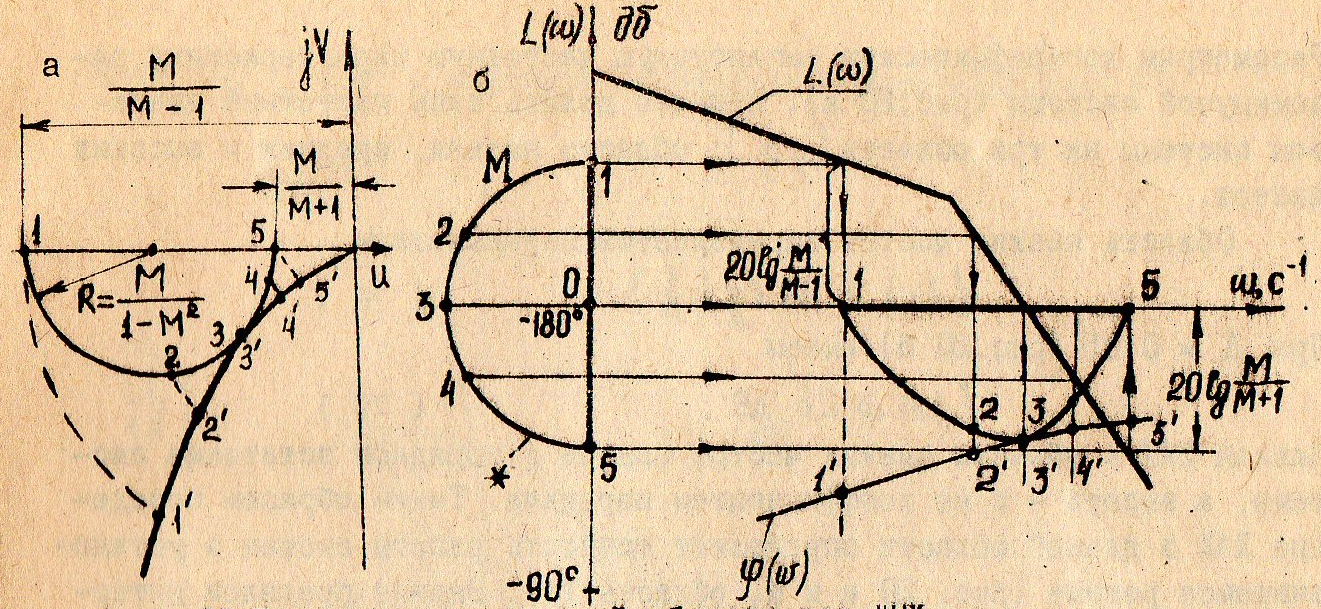
Рис. 22.18. Построение запретной области для ЛЧХ