Рассмотрим показатель точности – величину ошибки системы в установившемся режиме.
Данный режим наступает в системе после окончания переходного процесса, вызванного изменением задающего 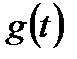 .
.
Если для системы стабилизации 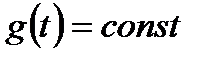 и для расчетов обычно используется
и для расчетов обычно используется 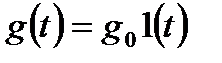 , то для программных и следящих систем
, то для программных и следящих систем
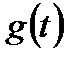 – изменяющаяся во времени величина и в качестве типовых используется
– изменяющаяся во времени величина и в качестве типовых используется 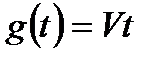 или
или 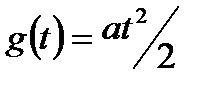 , где V и a – соответственно максимальные значения скорости и ускорения
, где V и a – соответственно максимальные значения скорости и ускорения 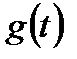 , имеющие место в реальном процессе. То же относится и к возмущающему воздействию
, имеющие место в реальном процессе. То же относится и к возмущающему воздействию 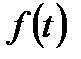 .
.
Графики переходных процессов систем при отработке различных задающих воздействий показаны в табл. 22.1.
Решим вопрос: одинаково ли легко добиться определенного значения ошибки 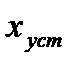 для различных
для различных 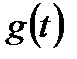 ? По-видимому, легче добиться определенной величины
? По-видимому, легче добиться определенной величины 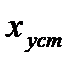 в случае
в случае  , т.е. когда задающее воздействие с течением времени остается постоянным, чем в случае изменяющегося задания. Иначе говоря, чем сложнее
, т.е. когда задающее воздействие с течением времени остается постоянным, чем в случае изменяющегося задания. Иначе говоря, чем сложнее 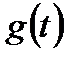 , тем система должна быть совершеннее по своим динамическим свойствам. На практике это значит, что система будет сложнее в техническом отношении, т.е. сложнее будет, например, регулятор и, следовательно, закон регулирования, реализованный в такой системе.
, тем система должна быть совершеннее по своим динамическим свойствам. На практике это значит, что система будет сложнее в техническом отношении, т.е. сложнее будет, например, регулятор и, следовательно, закон регулирования, реализованный в такой системе.
Как динамическая структура систем влияет на точность их работы?
Рассмотрим общий случай системы с передаточной функцией в разомкнутом состоянии 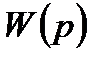 равной
равной
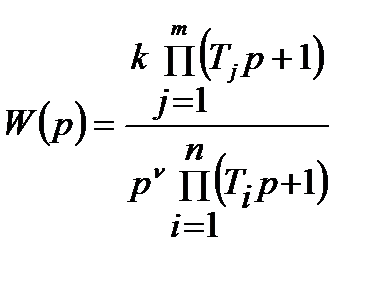 . (22.4)
. (22.4)
Для простоты положим, что передаточная функция в цепи обратной связи 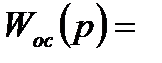 1.
1.
Это означает, что передаточная функция датчика перенесена в прямой канал разомкнутой системы и за выходную величину системы в этом случае принимается сигнал с датчика. Таким образом, исследованию подлежит не ошибка регулирования, а сигнал рассогласования. Поскольку в большинстве случает датчик – менее инерционное звено, чем объект управления, и обычно рассматривается как безинерционное звено, ошибка регулирования конкретной системы, соответствующая рассогласованию легко определяется через коэффициент передачи датчика
В дальнейших рассуждениях, с точки зрения смысла исследования, будем говорить не о рассогласовании, а об ошибке регулирования.
Исследуя ошибку системы в установившемся режиме, в качестве модели системы возьмем ее передаточную функцию по ошибке
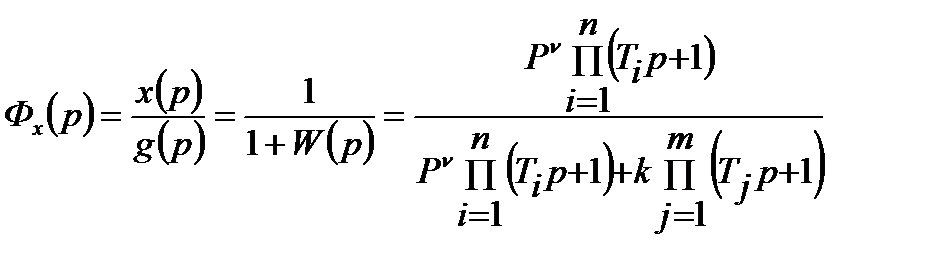 (22.5)
(22.5)
и, воспользовавшись предельной теоремой Лапласа, запишем
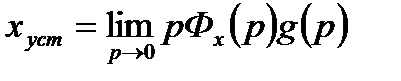 ,. (22.6)
,. (22.6)
где xуст – величина ошибки системы в установившемся режиме.
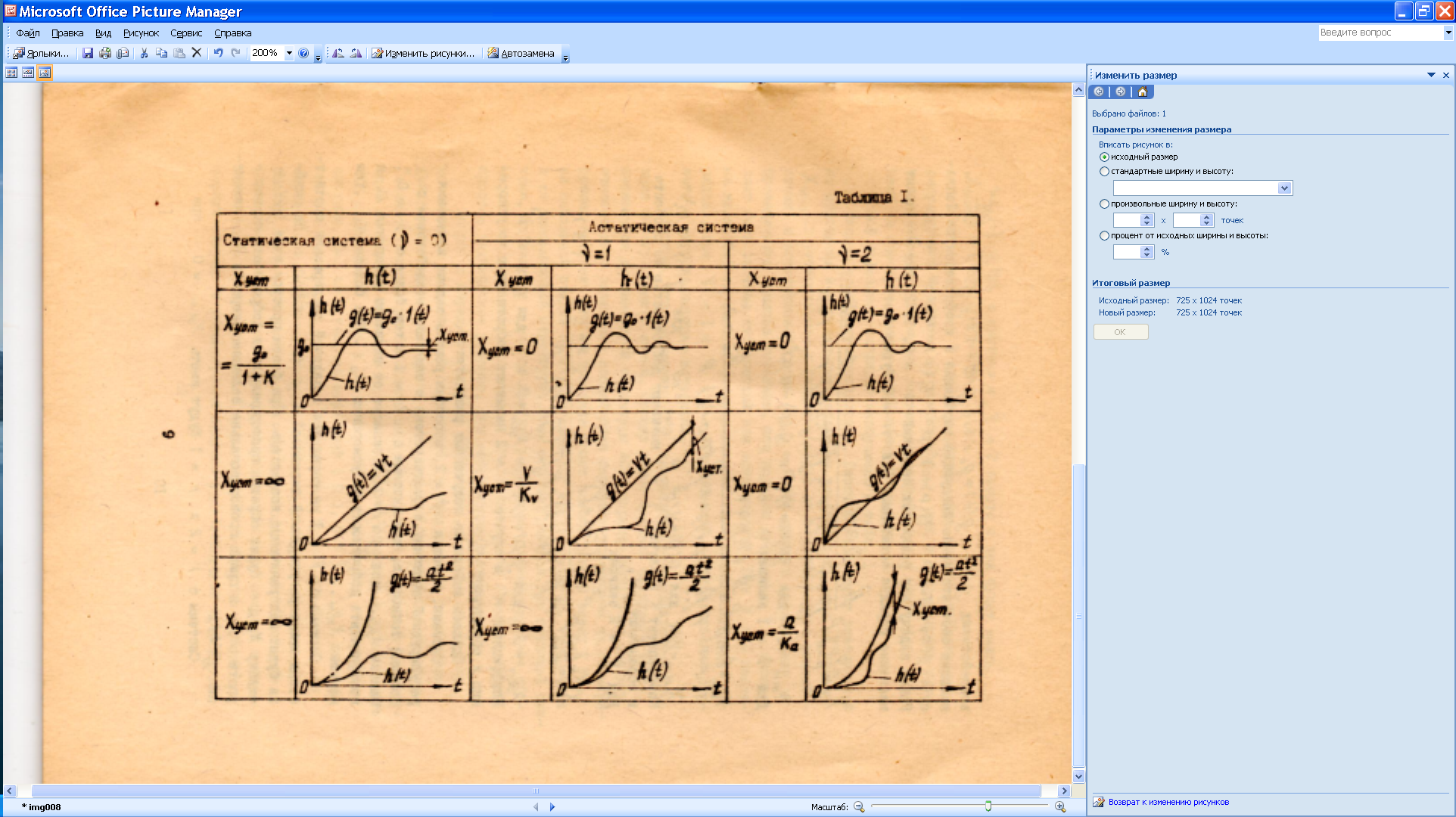
Рассмотрим точность работы систем при различных типовых задающих воздействиях: 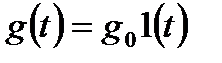 ;
; 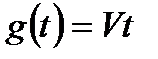 ;
; 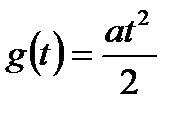 , имеющих соответственно следующие выражения в изображении по Лапласу:
, имеющих соответственно следующие выражения в изображении по Лапласу:
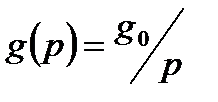 ;
; 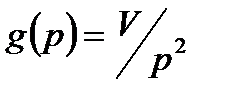 ;
; 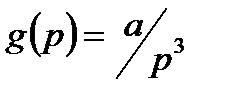 .
.
Решим задачу для различных значений показателя степени p в знаменателепередаточной функции системыn = 0, 1, 2, где n носит название «порядок астатизма».
Для n = 0 постоянного задающего воздействия будем иметь:
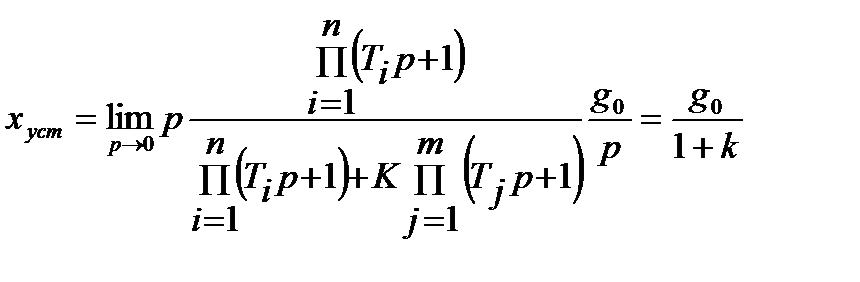 (22.7)
(22.7)
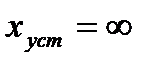 для
для 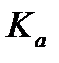 и
и 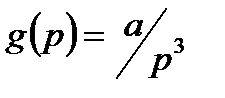 .
.
Для n = 1 запишем:
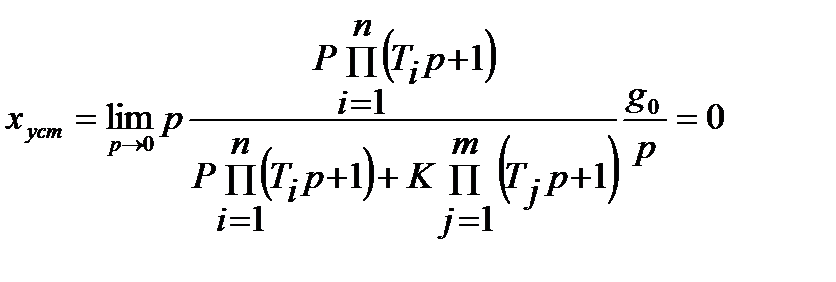 , (22.8)
, (22.8)
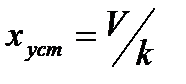 для
для 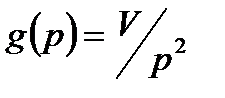 и
и 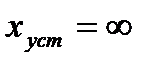 для
для 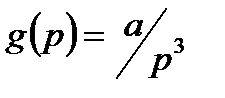 .
.
Коэффициент K в случае n = 1 называют добротностью по скорости и обозначают 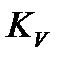 .
.
Для n = 2 запишем
 (22.9)
(22.9)
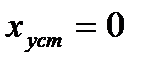 для
для 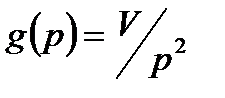 и
и 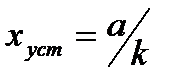 для
для 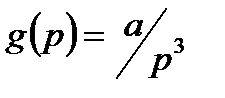 .
.
Коэффициент в случае n = 2 называют добротностью по ускорению и обозначают 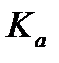 .
.
Сделаем выводы из полученных результатов.
Система, имеющая n = 2, способна решать задачи изменения регулируемой величины в соответствии с задающим воздействием с большей точностью, чем система с n = 1 и тем более с n = 0. Ошибка 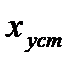 для
для 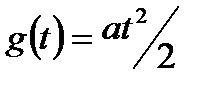 зависит от величины ускорения a и коэффициента добротности по ускорению
зависит от величины ускорения a и коэффициента добротности по ускорению 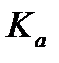 . Чем больше
. Чем больше 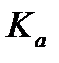 , тем меньше
, тем меньше 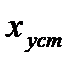 .
.
Система с n = 1 не справится с задачей поддержания соответствия между регулируемой величиной и 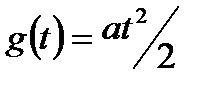 . Ее ошибка будет неограниченно возрастать. При более простом виде
. Ее ошибка будет неограниченно возрастать. При более простом виде 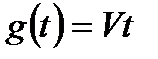 ошибка
ошибка 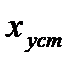 будет обратно пропорциональна добротности по скорости
будет обратно пропорциональна добротности по скорости 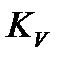 и прямо пропорциональна величине скорости V изменения
и прямо пропорциональна величине скорости V изменения 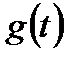 .
.
Системы с n = 2 и n = 1 будут иметь 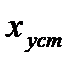 = 0 при g(t)=
= 0 при g(t)= 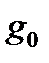 1(t), а система с
1(t), а система с 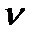 =2 вместе с тем будет иметь x
=2 вместе с тем будет иметь x  =0 и при g(t)=Vt.
=0 и при g(t)=Vt.
Система с 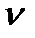 =0 способна решать лишь задачи стабилизации регулируемой величины. Ее ошибка x, как и в предыдущих случаях зависит от величины задающего воздействия и может быть изменена за счет увеличения коэффициента передачи К.
=0 способна решать лишь задачи стабилизации регулируемой величины. Ее ошибка x, как и в предыдущих случаях зависит от величины задающего воздействия и может быть изменена за счет увеличения коэффициента передачи К.
Все сказанное изображено в табл. 22.1.
Статическая система (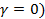 |
| Астатическая система |
Введем следующее определение. Система называется статической по отношению к постоянному задающему воздействию, если ее ошибка X  в установившемся режиме зависит от величины этого воздействия и астатической, если X
в установившемся режиме зависит от величины этого воздействия и астатической, если X  =0. Из данного определения и проведенного анализа вытекает, что порядок астатизма
=0. Из данного определения и проведенного анализа вытекает, что порядок астатизма 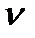 определяет, быть системе статической или астатической. При
определяет, быть системе статической или астатической. При 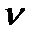 =0 система является статической
=0 система является статической
(иногда говорят астатической нулевого порядка), при 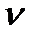 =1 и
=1 и 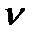 =2- астатической, соответственно первого и второго порядка астатизма.
=2- астатической, соответственно первого и второго порядка астатизма.
Заметим, что выражение 1/p соответствует передаточной функции интегрирующего звена. Отсюда можно сделать следующий вывод, касающийся динамической структуры ACP: порядок астатизма системы относительно задающего воздействия определяется числом ее интегрирующих звеньев. Чем на практике может помочь данный вывод? Уже на начальной стадии проектирования ACP можно поставить требования к ее динамической структуре: если это программа или следящая система, то наличие в ней по крайней мере одного интегрирующего звена обязательно, если этот система стабилизации, то возможно более простое техническое решение, без интегрирующих звеньев.
Вопрос о порядке астатизма ACP связан, как уже отмечалось, не только с динамической структурой системы, но и с характером действующих на нее сигналов. Вспомним, что при введении понятия "асимптотическая устойчивость систем" характер и величины действующих на систему сигналов не принимались во внимание и устойчивость ACP связывалась лишь с ее собственными свойствами, параметрами системы. Из выражений (22.7) - (22.9) для X при различных g(t) следует, что система, будучи устойчивой по определению, может на практике иметь неограниченно возрастающую ошибку X при изменяющемся задающем воздействии. Сказанное подчеркивает важность введения понятия астатизма системы при решении задач проектирования. Так, расчет ACP необходимо начинать, в первую очередь, с рассмотрения вопроса удовлетворения требований к точности ее работы, а затем уже решать вопросы, связанные с быстродействием и запасом устойчивости. 
Далее, если системы с астатизмом большего порядка обладают и большей точностью, почему бы это не учесть заранее введением дополнительных интегрирующих звеньев? Точность работы систем возможно удастся повысить, т.е. удастся уменьшить ошибку X  . Однако быстродействие и запас устойчивости системы при этом ухудшатся и система может стать даже неустойчивой. Объясняется это тем, что каждое интегрирующее звено вносит в систему отрицательный фазовый сдвиг -
. Однако быстродействие и запас устойчивости системы при этом ухудшатся и система может стать даже неустойчивой. Объясняется это тем, что каждое интегрирующее звено вносит в систему отрицательный фазовый сдвиг - 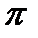 /2 и вместе с тем спектр частот, пропускаемых звеном, ограничен. Введение интегрирующего звена в систему позволяет уменьшить X
/2 и вместе с тем спектр частот, пропускаемых звеном, ограничен. Введение интегрирующего звена в систему позволяет уменьшить X  , но требуются, если нужно, дополнительные меры по сохранению или улучшению запаса устойчивости и быстродействия.
, но требуются, если нужно, дополнительные меры по сохранению или улучшению запаса устойчивости и быстродействия.
Отсюда следует, что получение более точной системы связано с ее усложнением и дополнительными затратами.
Как видно из приведенных рассуждений, при решении задач обеспечения требуемой точности ACP с одновременным обеспечением требуемого быстродействия и запаса устойчивости возникают противоречия, которые приходится разрешать в процессе проектирования систем.
Для определения ошибки X 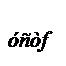 от возмущающего воздействия следует также воспользоваться предельной теоремой Лапласа:
от возмущающего воздействия следует также воспользоваться предельной теоремой Лапласа:
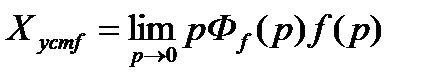 . (22.10)
. (22.10)
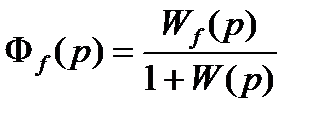 . (22.11)
. (22.11)
Система будет иметь 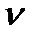 -й порядок астатизма по возмущающему воздействию, если ее передаточная функция Ф
-й порядок астатизма по возмущающему воздействию, если ее передаточная функция Ф 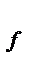 (р) будет иметь в числителе pν, т.е. нуль кратности
(р) будет иметь в числителе pν, т.е. нуль кратности 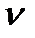 .
.
Так, если предположить, что
 . (22.12)
. (22.12)
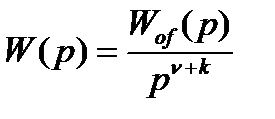 . (22.13)
. (22.13)
где 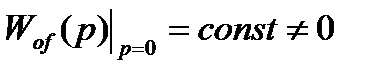 ,
, 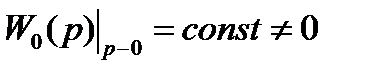 ,
,
то 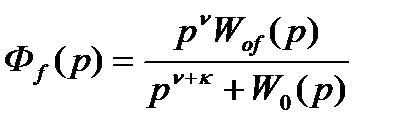 . (22.14)
. (22.14)
Отсюда, если W 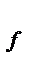 (р) имеет сомножителем 1/р
(р) имеет сомножителем 1/р 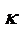 ,то для того, чтобы замкнутая система обладала астатизмом
,то для того, чтобы замкнутая система обладала астатизмом 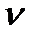 - того порядка относительно возмущающего воздействия, необходимо, чтобы W(р) содержала множитель 1/р
- того порядка относительно возмущающего воздействия, необходимо, чтобы W(р) содержала множитель 1/р 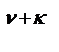 .
.
В целом ошибка в установившемся режиме X(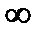 ) в силу принципа суперпозиции равна сумме ошибок от задающего X
) в силу принципа суперпозиции равна сумме ошибок от задающего X  и возмущающего X
и возмущающего X  воздействий:
воздействий:
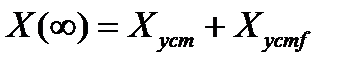 (22.15)
(22.15)
В то время как указанные составляющие ошибки можно изменять в процессе проектирования ACP, существует ошибка чувствительного элемента Xчэ, которую устранить невозможно. но которую следует учитывать при оценке точности работы систем:
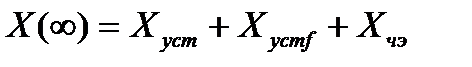 (22.16)
(22.16)
Порядок астатизма по задающему и возмущающему воздействиям в общем случае может быть неодинаков. Отсюда следует заключить, что при проектировании системы, для повышения точности ее работы, необходимо учитывать, какой из режимов работы является для нее наиболее характерным.
Заметим, что формулы для определения ошибки X  могут быть использованы не только при решении задач анализа точности системы, но и при отыскании коэффициента передачи системы, при котором данная ошибка будет меньше или равна своему требуемому значению X
могут быть использованы не только при решении задач анализа точности системы, но и при отыскании коэффициента передачи системы, при котором данная ошибка будет меньше или равна своему требуемому значению X  , задаваемому при проектировании.
, задаваемому при проектировании.
Для статических систем, астатических 1-го и 2-го порядка по задающему воздействию можно соответственно записать условия, при которых
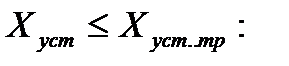

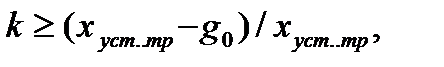
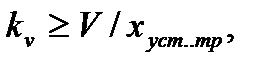
k 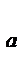
 .
.
Аналогичные неравенства можно получить и для возмущающего воздействия.
 2015-04-17
2015-04-17 1027
1027
