Известно, что корни характеристического уравнения системы зависят от ее параметров и определяют характер протекающих в ней переходных процессов [1]. Отсюда возникает возможность судить по данным корням о быстродействии и запасе устойчивости системы.
Чем меньше вещественная часть корня, тем медленнее затухает соответствующая ему составляющая переходного процесса. Вместе с тем наличие комплексных корней приводит к появлению в переходном процессе составляющих колебательного характера.
Рассмотрим в качестве примера систему, структурная схема которой показана на рис.22.2.
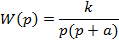
|
g(p) x(p) y(p)
Рис. 22.2. Структурная схема системы
Изображение регулируемой величины системы определим как:
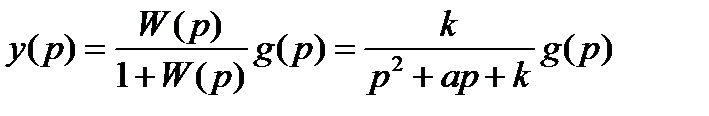 . (22.17)
. (22.17)
Используя стандартную форму записи, запишем:
y(p) = 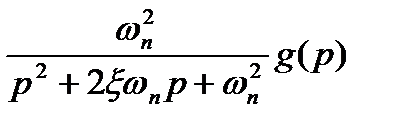 . (22.18)
. (22.18)
Переходная функция системы (при g(p)= 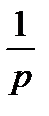 ) будет:
) будет:
y(t)= 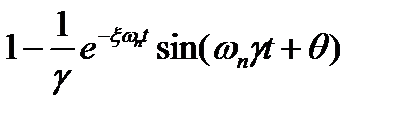 , (22.19)
, (22.19)
где 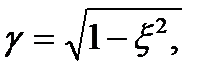
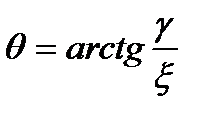
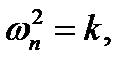
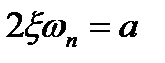 .
.
Переходные функции для различных ξ показаны на рис. 22.4.
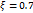
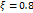
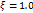
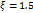
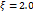
|

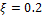
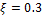
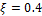
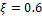
|
| y(t) |
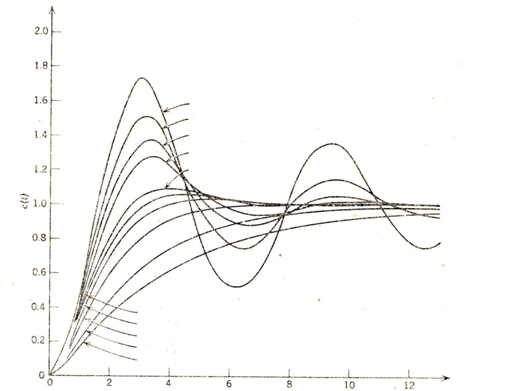
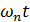
Рис. 22.3. Переходные функции системы
Корни характеристического уравнения системы
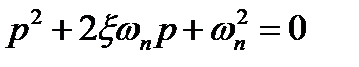 (22.20)
(22.20)
равны
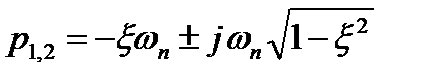 (22.21)
(22.21)
Расположение их на комплексной плоскости показано на рис. 22.4.
j 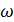 j
j 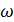

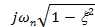 x
x 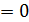
x 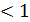
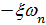
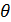 x
x 
x= 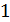
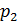 -
- 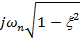
а б
Рис. 22.4. Плоскость корней Рис. 22.5. Кривая корней при
изменении ξ
На рис. 22.5 показана кривая – геометрическое место точек, соответствующих различным значениям корней при изменении ξ.
Как следует из сравнения рис. 22.3 и рис. 22.4, – расположение корней на комплексной плоскости однозначно связано с характером переходного процесса в системе. Рассмотрим связь перерегулирования σ и времени первого максимума tм с параметром затухания ξ. Дифференцируя выражение (22.19) и полагая производную равной нулю, получим
при ωп γ t = π:
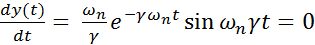 . (22.22)
. (22.22)
Отсюда 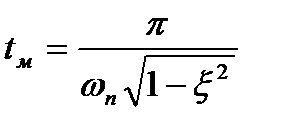 (22.23)
(22.23)
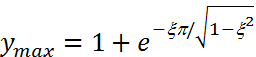 (22.24)
(22.24)
и, следовательно
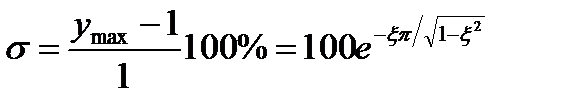
. (22.25)
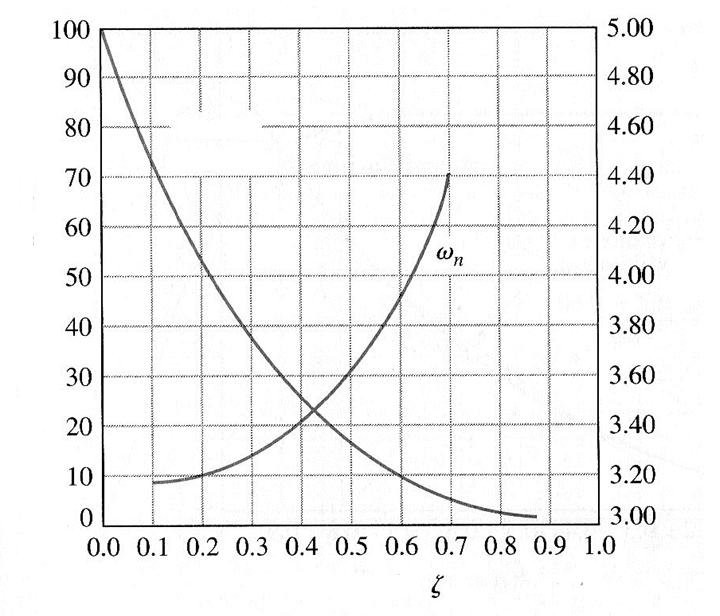
Зависимости для σ и ωn tм от ξ противоположны: чем больше ξ, тем меньше σ и больше ωn tм.

|
| σ |

|
| σ |

|
| σ |
Рис. 22.6. Зависимость σ и 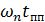 от ξ
от ξ
Данными зависимостями можно воспользоваться и для системы третьего порядка с передаточной функцией:
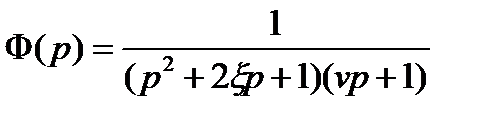 (22. 26)
(22. 26)
Если выполняется условие:
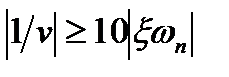 (22. 27)
(22. 27)
Другими словами поведение системы третьего порядка может быть рассмотрено как поведение системы второго порядка, если вещественная часть ближайших к минимальной оси корней по модулю в 10 раз меньше вещественной части третьего корня.
Рассмотрим связь затухания ψ за период с расположением корней на комплексной плоскости. Для этого воспользуемся выражением (22.22) и найдем затухание амплитуды синусоидального колебания за период. В некоторый момент времени t1при ymax эта амплитуда будет равна
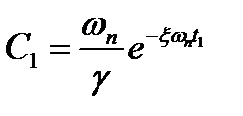
(22.28)
Спустя один период T = 2π/ωпg получим
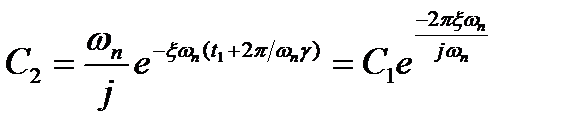 (22.29)
(22.29)
На основании выражений (22.28) и (22.29) запишем
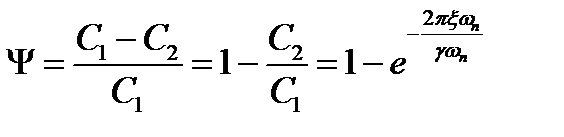
(22.30)
Если в выражении (22.30) ввести обозначения
gwn =α и 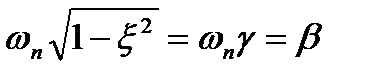 , (22.31)
, (22.31)
где α– вещественная, а β – мнимая части корней (β называется также частотой затухающих колебаний), то уравнение (22.30) можно переписать в виде
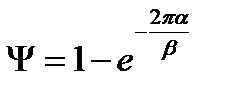
. (22.32)
Отношение β/α = μ называют к о л е б а т е л ь н о с т ь ю. Перепишем выражение (22.3.16):
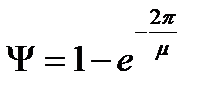
. (22.33)
Отсюда можно получить:

. (22.34)
Для рассматриваемой системы имеем
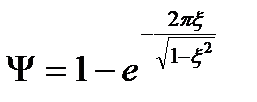
. (22.35)
Из выражений (22.25), (22.34) и (22.35 можно получить еще несколько дополнительных соотношений:
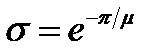 (22.36)
(22.36)
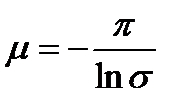
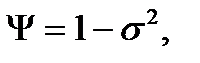 . (22.37)
. (22.37)
(22.38)
где σ берется в относительных единицах.
Анализируя полученные зависимости можно отметить, что при проектировании систем задача выполнения требований к σ и tм противоречива (рис. 22.6).
Так, например, при увеличении ξ перерегулирование σ уменьшается, и время максимума tм увеличивается. Решение задачи заключается в отыскании компромиссного решения с учетом степени важности σ и tм для системы.
Рассмотрим вновь уравнение для переходного процесса системы n – ного порядка:
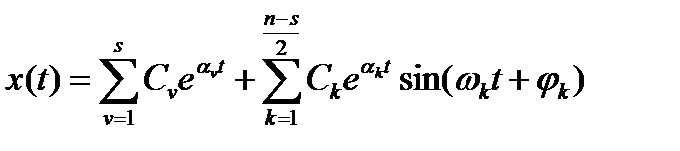 . (22.39)
. (22.39)
Скорость затухания каждого из слагаемых определяется величиной вещественной части корня α. Чем меньше α (чем ближе корень расположен к мнимой оси), тем больше время затухания слагаемого. Проанализируем, как связана скорость затухания x(t) (время переходного процесса tпп) со скоростью затухания каждого из слагаемых выражения (22.39).
Решим более общий вопрос: как инерционность целого зависит от инерционности составляющих это целое частей? Рассмотрим в качестве аналогии отряд, состоящий из пеших и велосипедистов. Ясно, что максимальная скорость движения всего отряда определяется максимальной скоростью передвижения наиболее инерционной его части – пеших. Рассуждая по аналогии, можно сделать вывод, что время переходного процесса tпп будет в основном зависеть от абсолютного значения вещественной части ближайшего к мнимой оси корня
(рис. 22.6), называемый степенью устойчивости η.
j (C1ep1t + C2ep2t)
C1ep1t
p1 p2 C2ep2t
0 t
h
Рис. 22.7. Влияние расположения корней на tпп.
В том случае, когда выполняется условие (22.27), можно по η определить приближенно время переходного процесса:
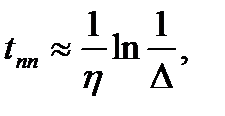
(22.40)
где в качестве Δ можно взять (0,02÷0,05) от установившегося значения регулируемой величины y( ).
).
Так при Δ = 0,05
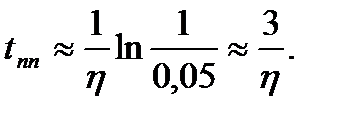
(22.41)
Данная оценка tпп, пусть и приближенная, часто достаточна для проектировщика при определении быстродействия системы. Вместе с тем tпп, вычисленная по формуле (22.41) может служить для проверки правильности определения tпп, например, временными методами.
Вернемся к рассматриваемой в качестве примера системе
(рис. 22.3.1).
Для нее η = x ωn. При Δ = 0,02 будем иметь.
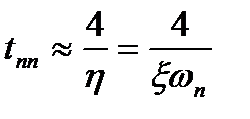
. (22.42)
Решим небольшую задачу по проектированию.
Пусть необходимо так выбрать коэффициент k и параметр a системы, чтобы ее перерегулирование было не более 5 %, а время переходного процесса было менее 4с.
Воспользуемся выражением (22.25), из которого для σ = 5% получим 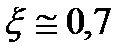 .
.
Далее воспользуемся уравнением (22.41), откуда
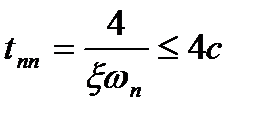
(22.43)
и следовательно
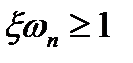
(22.44)
На плоскости корней два ограничения в виде неравенств (22.43) и (22.44) отображаются в виде заштрихованной области (рис. 22.8).
Выберем корни непосредственно на границе. Тогда Р1 = –1 + j1 и
Р2 = – 1 – j1. Из (22.43) и (22.44) получим, что 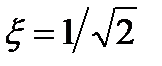 и
и 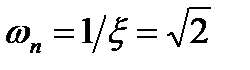 .
.
Отсюда для передаточной функции системы
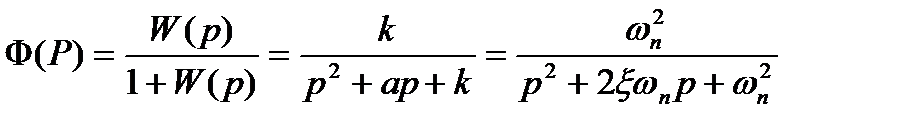 (22.45)
(22.45)
найдем, что 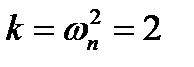 и
и 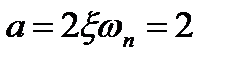 .
.
j
p1
450
p2 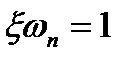
Рис. 22.8. Область расположения корней
Заметим, что в данном случае 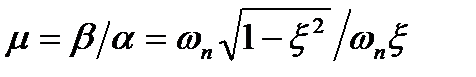 соответствует геометрически тангенсу угла
соответствует геометрически тангенсу угла  (рис. 22.8), т.е.
(рис. 22.8), т.е. 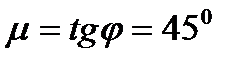 , а
, а 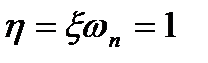 .
.
Из примера видно, что колебательность μ и степень устойчивости η могут использоваться не только для оценки качества работы уже имеющейся системы, но также и для постановки требований и качеству проектируемых систем.
Для систем, описываемых уравнением порядка n>2, переходные процессы имеют вид, схожий с переходными процессами для систем 2-го порядка.
 2015-04-17
2015-04-17 524
524








