2015-04-17
2089
Рассмотрим законы движения электронов в различного рода электрических и магнитных полях применительно к одному дискретному электрону, проявляющему главным образом корпускулярные свойства. Наука о законах движения заряженных частиц в электрических и магнитных полях называется электронной оптикой. Это название не случайно, так как между движением заряженных частиц в полях и распространением света в оптических средах существует весьма тесная аналогия. Эта аналогия основана на тождестве основных законов световой и электронной оптики.
При движении электрона в электрических полях в качестве показателя преломления используется безразмерная величина
,
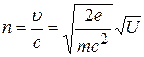где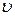 
— скорость электрона; с — скорость света; U — потенциал в данной точке поля.
Если электрон перемещается в магнитных полях, то показатель преломления n является функцией не только скорости электрона 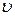, но и зависит от направления его движения по отношению к вектору напряженности H магнитного поля, что можно сравнить с распространением светового луча в анизотропных оптических средах.
Законы движения электрона тождественны известным законам световой оптики. Однако, пользуясь указанной аналогией, следует помнить и о ряде особенностей, отличающих электронную оптику от световой.
Потенциал электрического поля, а следовательно, и показатель преломления может непрерывно изменяться, в то время как в световой оптике показатель преломления обычно меняется скачкообразно на границе двух сред. Изменение потенциала поля меняет кинетическую энергию электрона; энергия же светового потока остается прежней, если пренебречь незначительными потерями на отражение, поглощение и рассеяние. В электронной оптике диапазон изменения показателя преломления значительно больше, чем световой, где n обычно находится между 1 и 2,5. Кроме того, в электронной оптике можно легко менять показатель преломления за счет изменения потенциалов различных электродов.
Все эти и некоторые другие особенности электронной оптики свидетельствуют о широких возможностях осуществления электронно-оптических приборов.
1 Движение электронов в однородном электрическом по ле
Предположим, что электрическое поле образовано плоским конденсатором, подключенным к батарее, с разностью потенциалов U. Размеры пластин конденсатора достаточно велики для того, чтобы пренебречь краевым эффектом и в рассматриваемом объеме считать электрическое поле однородным.
Как известно, электрон в однородном электрическом поле подвергается воздействию постоянной силы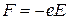 
. Согласно второму закону Ньютона эта сила равна:
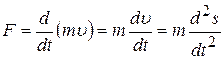. (1)
Отсюда общее уравнение движения электрона в электрическом поле имеет вид:
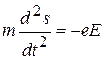. (2)
Это общее уравнение можно написать в виде проекций отрезка пути и вектора напряженности поля на оси координат:
, 
, 
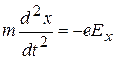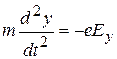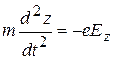. (З)
Расположим ось координат, как показано на рис. 1, и рассмотрим случай, когда электрон входит в однородное поле из качала координат (х = 0, y = 0, z = 0). Вектор его начальной скорости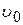 
лежит в плоскости хОz и составляет с положительной осью z угол q. Отсюда составляющие начальной скорости электрона по осям:
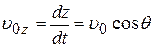и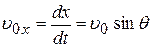 
.
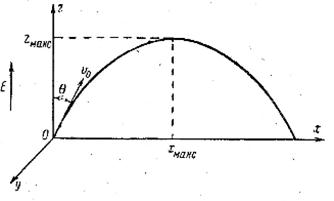
Рис. 1. Движение электрона в однородном электрическом поле.
Вектор напряженности поля параллелен оси z, и следовательно, Ех = 0, Eу = 0, Ez = E. Электрон, очевидно, будет двигаться в плоскости xOz. Следовательно, уравнения движения электрона принимают вид:
, 
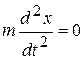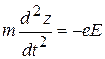. (4)
Интегрируя эти уравнения, получим:
, 
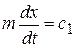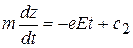. (5)
Постоянные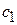 
и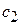 
можно определить, положив t = 0. Тогда составляющие скорости электрона по осям будут равны составляющим его начальной скорости :
, 
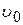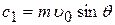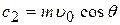. (6)
Таким образом, составляющие скорости в процессе движения
, 
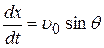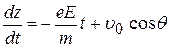. (7)
Интегрируя повторно, получим:
, 
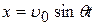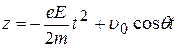. (8)
Постоянные интегрирования при этом, очевидно, равны нулю, так как в момент t = 0 электрон находился в начале координат (х = 0, z = 0).
Согласно (8)
.
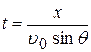Подставляя это выражение в (8), получим:
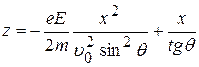, (9 а)
или
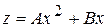(9 б)
где
, 
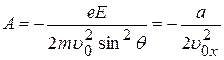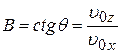. (10)
В выражении (10) величина (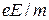
) обозначена через а. Она определяет ускорение электрона в соответствии с аналогией уравнения (8) уравнению равнозамедленного движения тела.
Представляет интерес, встречающийся в ряде электронных приборов случай,когда вектор начальной скорости электрона 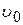нормален к вектору напряженности поля Е: 
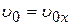. По-прежнему в момент t = 0 электрон находится в начале координат (х = 0, у = 0, z = 0) и
, 
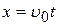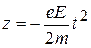. (11)
Определяя из первого уравнения время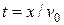 
и подставляя его во второе уравнение, получим:
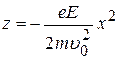. (12)
Электрон будет двигаться в плоскости xOz по параболе, отклоняясь от оси х под воздействием ускоряющего поля Е (рис. 2). Этот случай движения электрона характерен для электроннолучевых приборов, в которых поперечное поле используется для отклонения электронного потока.
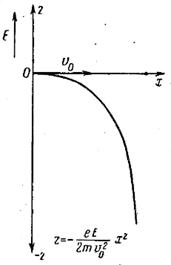
Рис. 2. Движение электрона в однородном электрическом поле в случае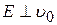 
.
Для определения траектории движения электрона в электрическом поле можно применить законы электронной оптики, используя отмеченную выше аналогию между электрическими полями и оптическими средами. Пусть, например, вектор начальной скорости 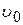электрона направлен под углом q 1 к вектору напряженности электрического поля Е (рис. 3).
Выделим элементарный участок поля, на котором потенциал изменяется от U 1 до U 2. Ввиду однородности поля эквипотенциальные поверхности (поверхности, все точки которых обладают одним и тем же потенциалом) U 1 и U 2 являются плоскостями. При движении электрона из точки 1 в точку 2 под воздействием ускоряющего электрического поля увеличивается составляющая его скорости, нормальная к эквипотенциальным плоскостям: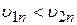 
. Тангенциальная же составляющая его скорости остается неизменной: 
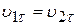. Вследствие этого угол между вектором скорости электрона и нормалью к эквипотенциальным плоскостям изменяется: 
.
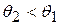Из условия равенства тангенциальных составляющих скорости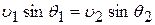 
можно получить:
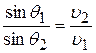, (13)
или
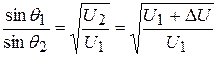. (14)
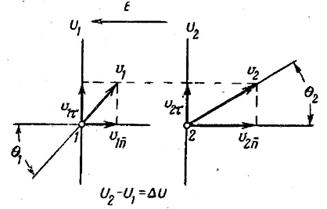
Рис. 3. Изменение составляющих скорости электрона при его движении в электрическом поле.
Выражение (13) аналогично формуле преломления светового луча на границе оптических сред:
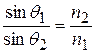, (15)
где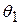 
и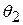 
— угол падения и угол преломления светового луча соответственно, а 
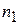и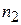 
— коэффициенты оптической плотности двух сред.
Пользуясь выражением (14), легко найти „угол преломления" для плоского конденсатора, который является „преломляющей призмой" (рис. 4). В этом случае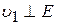 
и
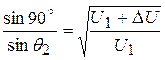, (16)
или
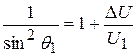. (17)
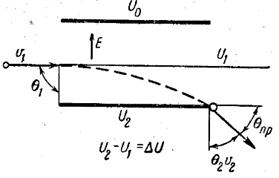
Рис. 4. Движение электрона в поле плоского конденсатора.
Отсюда легко определить угол преломления:
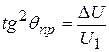. (18)
2. Движение электронов в неоднородном электрическом поле
В электронных приборах электростатические поля обычно создаются совокупностью различных по форме электродов, которые находятся под тем или иным потенциалом. Как правило, такие поля являются неоднородными, и если в пространстве нет других зарядов, то такое электростатическое поле описывается уравнением Лапласа:
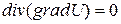. (19)
Решение этого уравнения в общем виде практически невозможно, а для более простых случаев, например аксиально-симметричных полей, встречает серьезные затруднения.
На практике конфигурация неоднородных электростатических полей определяется экспериментально. Одним из наиболее распространенных является метод электролитической ванны, заключающийся в следующем. В плоскую ванну (рис. 5), выполненную из диэлектрического материала, помещают модели электродов. Конфигурация их и взаимное расположение в точности соответствуют конфигурации и расположению электродов в приборе, поле в котором подлежит исследованию. При этом все линейные размеры могут быть увеличены в n раз, что при полном геометрическом подобии поля приведет лишь к уменьшению напряженности в любой точке поля в 1/ n раз. Моделям электродов сообщаются потенциалы, равные или в m раз большие истинных потенциалов в приборе. Пропорциональное увеличение потенциалов на всех электродах также не нарушает конфигурации поля и приводит лишь к увеличению напряженности поля в m раз.
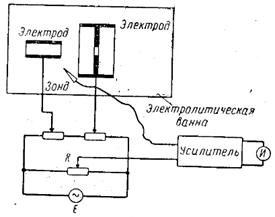
Рис. 5. Устройство электролитической ванны.
Ванна с электродами наполняется каким-либо электролитом, обычно водой. Для исключения влияния электролиза на проводимость электролита к электродам обычно подводят переменное напряжение (генератор E). К токопроводящему зонду от того же генератора с делителя R подается регулируемое переменное напряжение. В цепь зонда включается усилитель с нуль-индикатором на выходе. Если зонд опустить в какую-либо точку ванны, то в цепи зонда потечет ток, обусловленный разностью потенциалов между данной точкой поля и зондом. Регулируя потенциометром R напряжение, подводимое к зонду, можно добиться равенства потенциалов и, следовательно, отсутствия тока в цепи зонда. Фиксируя точки поля с одинаковым потенциалом, получают сечение одной из эквипотенциальных поверхностей. Измерения повторяют при различных напряжениях зонда и строят семейство эквипотенциальных кривых.
Зная картину неоднородного электрического поля, можно воспользоваться методами графического построения траекторий электронов. Один из этих методов, основанный на законе преломления, заключается в построении траектории электрона в виде ломаной линии, отрезки которой ограничены соседними эквипотенциальными поверхностями. Изменение направления движения электрона для случая, показанного на рис. 3, можно определить, воспользовавшись соотношением (14). Однако обычно разность потенциалов для соседних эквипотенциальных поверхностей невелика и оперирование с синусами малых углов, а также геометрическое построение этих углов затруднительны.
Один из практических методов построения траектории электрона иллюстрируется рис. 6.
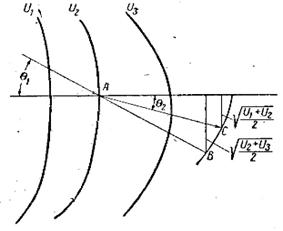
Рис. 6. Построение траектории движения электрона в неоднородном электрическом поле.
Направление движения электрона, падающего на поверхность U 1 под углом q1, продолжают до точки В, отстоящей от нормали к поверхности U 1 на величину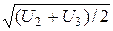 
. Затем из точки А через точку В проводят дугу окружности и отмечают на ней точку С, отстоящую от нормали на величину 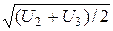. Соединив точки А и С, определяют направление движения электрона между поверхностями U 2 и U 3. Продолжив построение для следующих пар эквипотенциальных поверхностей, получают траекторию электрона в неоднородном поле в виде ломаной линии, которую без существенной погрешности можно заменить плавной кривой. Неоднородные электрические поля, широко используемые в электронных приборах для изменения скорости и направления движения электронов, называются электронными линзами. В электронной оптике различают линзы-диафрагмы, одиночные линзы, иммерсионные линзы и иммерсионные объективы.
Примеры линз-диафрагм показаны на рис. 7; там же приведены кривые распределения потенциалов вдоль оси линзы. Линзы-диафрагмы, образованные электродами с круглыми отверстиями, могут быть собирающими и рассеивающими. В собирающей линзе в плоскости диафрагмы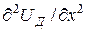 
> 0; в рассеивающей линзе, наоборот, 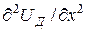< 0. Фокусное расстояние линз-диафрагм можно определить по формуле
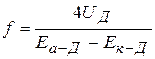, (20)
где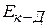 
— напряженность поля слева, а 
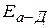— справа от диаграммы.
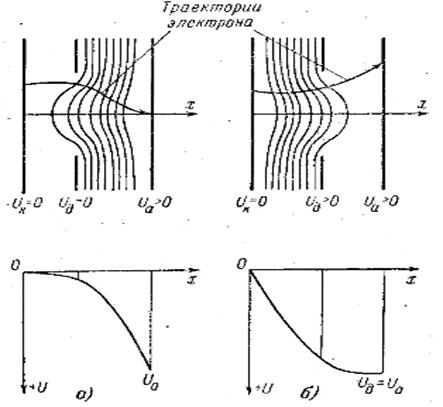
Рис. 7. Электронные линзы — диафрагмы и распределение потенциала в них: а — собирающая; б — рассеивающая.
Одиночные линзы образуются системой линз-диафрагм и характеризуются постоянными и равными потенциалами по обе стороны линз. Пример одиночной линзы показан на рис. 8.
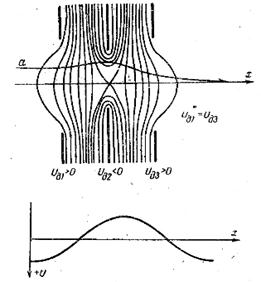
Рис. 8. Одиночная электронная линза и распределение потенциала в ней
3. Движение электронов в однородном магнитном поле
Перемещение электрических зарядов в магнитном поле при условии, что траектория движения заряда пересекает силовые линии поля, определяется силой, действующей на этот заряд:
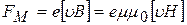. (21)
В международной системе единиц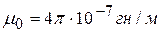 
. Для вакуума 
.
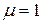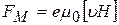. (22)
Вектор силы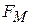 
нормален к плоскости, в которой расположены векторы — сомножители 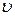и Н. Направление вектора 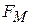— силы Лоренца легко найти, пользуясь правилом правой руки.
Рассмотрим, какая работа затрачивается при перемещении электрона в магнитном поле:
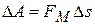. (23)
Подставляя сюда (22) и учитывая, что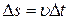 
, получим:
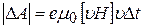, (24)
так как скалярное произведение двух взаимно перпендикулярных векторов FM и 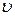равно нулю.
Это означает, что кинетическая энергия электрона при его движении в магнитном поле остается неизменной. Другими словами, магнитное поле не может замедлить или ускорить движение электронов. Из выражения (22): На электрон, находящийся в покое, движущийся параллельно силовым линиям, магнитное поле не оказывает никакого воздействия (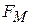 = 0). Оно может изменить направление движения электрона и только в том случае, если начальная скорость электрона не равна нулю, и при своем движении он пересекает силовые линии магнитного поля.
Используя проекции векторов 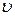и Н на оси координат, можно выражение (22) записать в виде:
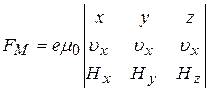. (25)
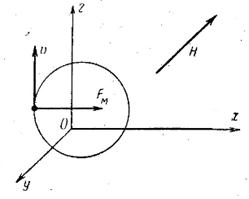
Рис. 9. Движение электрона в однородном магнитном поле
в случае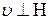 
.
Раскрывая детерминант и учитывая, что F = ma, получим выражение для составляющих силы FM по осям координат:
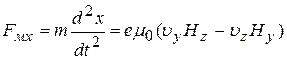, (26a)
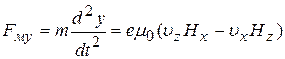, (26б)
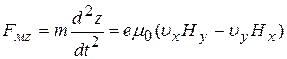. (26в)
Рассмотрим случай, когда вектор скорости электрона 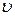нормален к силовым линиям магнитного поля Н. Как видно из рис. 9:
, 
,
, 
,
, 
.
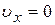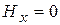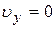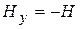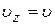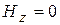При этом условии система уравнений (26) примет вид:
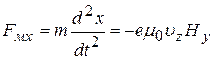, (27а)
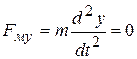, (27б)
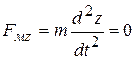. (27в)
На электрон действует сила, направленная вдоль оси х:
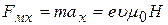. (28)
Эта сила сообщает электрону ускорение, вектор которого совпадает с направлением силы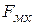 
и, следовательно, перпендикулярен 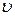. Отсюда видно, что ускорение 
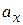является центростремительным и движение электрона происходит по криволинейной траектории.
Таким образом,
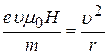(29)
и отсюда
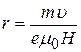. (30)
Здесь m = const; e = const, Н = const, так как поле однородно, и 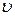=const. Таким образом, радиус кривизны траектории также остается неизменным: r = const. Этому условию удовлетворяет только окружность.
Рассмотрим более общий случай, когда вектор скорости электрона не лежит ни в одной из координатных плоскостей, а вектор напряженности поля Н направлен вдоль одной из осей, например, вдоль оси х (рис. 10). Спроектируем вектор начальной скорости электрона на координатные оси. В этом случае уравнения (26) запишутся в виде
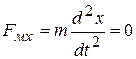, (31а)
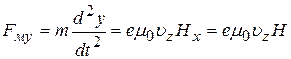, (31б)
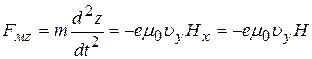. (31в)
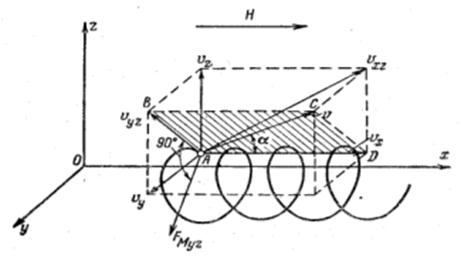
Рис. 10. Общий случай движения электрона в однородном магнитном поле.
Обе действующие на электрон силы лежат в плоскости уОz. Суммарная сила, действующая на электрон, перпендикулярна плоскости ABCD, содержащей векторы Н и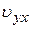 
, и определяется из соотношения
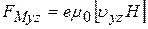. (32)
Под действием этой силы электрон вращается по окружности, лежащей в плоскости yOz. Кроме того, под действием составляющей начальной скорости, направленной вдоль оси х, электрон движется поступательно вдоль этой оси. Результирующей траекторией электрона является спираль, ось которой параллельна оси х, а радиус витка в соответствии с (30) равен:
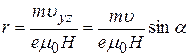. (33)
Один оборот спирали электрон совершит за время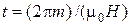 
, переместясь со скоростью 
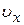вдоль оси х на шаг спирали:
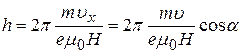. (34)
Однородное магнитное поле в некоторых электроннолучевых приборах используется в качестве магнитной электронной линзы, фокусирующей поток электронов, выходящий с поверхности катода под некоторым углом 2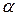 
(рис. 11).
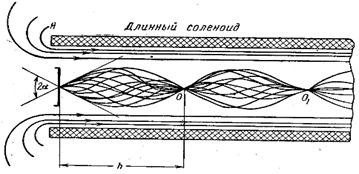
Рис. 11. Магнитная линза, образованная полем длинной катушки.
Если угол 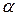невелик, то такой пучок электронов называют параксиальным. Фокусирующее действие однородного магнитного поля, создаваемого обычно длинным соленоидом, основано на равенстве шага спиральных траекторий всех электронов. Уго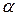л мал,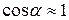 
, и шаг спирали
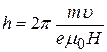(35)
не зависит от направления вектора начальной скорости электронов. В точках О, О 1 и др., отстоящих друг от друга на величину h, траектории электронов касаются оси соленоида. Происходит фокусирование электронного пучка.
4. Движение электронов в неоднородном магнитном поле
Задача аналитического описания неоднородных магнитных полей встречает не меньшие трудности, чем в случае неоднородного электрического поля. Поэтому для определения картины неоднородного магнитного поля применяются, как правило, экспериментальные методы. Один из наиболее простых и распространенных — баллистический метод. Небольшую катушку, к которой подключен баллистический гальванометр, помещают в выбранную точку магнитного поля, так чтобы ось катушки совпадала с направлением магнитных силовых линий. Затем катушку быстро удаляют из поля и по величине наведенной в катушке э.д.с. находят напряженность поля в данной точке. Построенные по точкам силовые линии неоднородного поля используются для определения траектории электрона при его движении в этом поле.
Неоднородные магнитные поля создаются для фокусирования параксиальных пучков электронов. Обычно используются короткие катушки – многослойные соленоиды, длина которых соизмерима с внутренним диаметром.
Рассмотрим движение электрона в неоднородном магнитном поле такой катушки (рис. 12).
Вектор скорости электрона направлен под углом 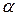к оси катушки. Разложим вектор Н напряженности магнитного поля в точке А на радиальную Нr и аксиальную На составляющие. Уго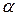л мал, 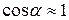, и можно считать, что 
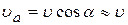. На электрон действует сила 
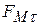(рис. 12,б), перпендикулярная плоскости чертежа и вызывающая вращательное движение электрона вокруг оси катушки. Под действием этой силы появляется тангенциальная составляющая скорости электрона 
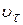(рис. 12,в), которая совместно с На образует силу 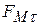, прижимающую электрон к оси. Таким образом, в неоднородном магнитном поле электрон движется по спирали с уменьшающимся радиусом и в некоторой точке С его траектория соприкасается с осью катушки.
Фокусное расстояние такой магнитной линзы, если пучок падающих электронов считать параллельным, определяется выражением:
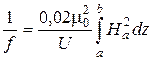, (36)
где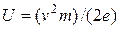 
- потенциал, определяющий скорость движения электрона вдоль оси катушки, а интегрирование осуществляется вдоль оси в пределах a-b неоднородного магнитного поля.
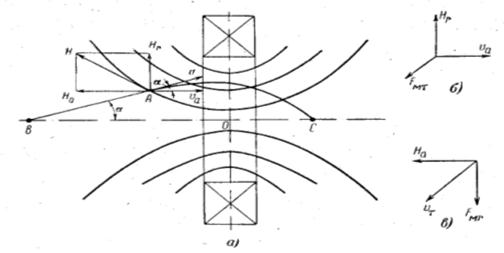
Рис. 12. Магнитная линза, образованная полем короткой катушки. а — магнитное поле; б и в — векторные диаграммы.
Если U выражено в вольтах, а Н — в эрстедах, то фокусное расстояние поучается в сантиметрах. Такая линза всегда является собирающей, так как ее оптическая сила не зависит от направления силовых линий поля.
5. Движение электронов в скрещенных электрическом и магнитном полях
Скрещенные электрическое и магнитное поля используются для управления электронным потоком во многих электронных приборах. В этом случае сила, действующая на' электрон, равна сумме сил действия электрического и магнитного полей в отдельности:
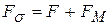, (37)
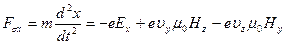, (38а)
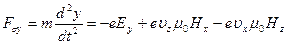, (38б)
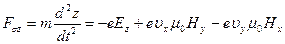. (38в)
Рассмотрим частный случай движения электрона в суммарном поле, когда векторы Е и H взаимно перпендикулярны. Электрическое поле образовано двумя плоскими параллельными электродами к и а (рис. 13), разность потенциалов которых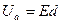 
, где d - расстояние между электродами;
; ;
; ;
; .
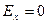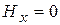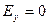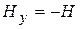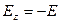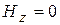Электрон находится в начале координат (x=y=z=0), его начальная скорость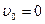 
и уравнения (38) принимают вид:
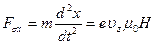, (39а)
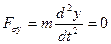, (39б)
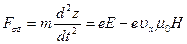. (39в)
Движение электрона будет происходить в плоскости хОу.
Рис. 13. Движение электрона во взаимно перпендикулярных
однородных электрическом и магнитном полях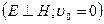 
.
Рассмотренные нами случаи окажутся весьма полезными при изучении движения электронов в сверхвысокочастотных генераторах — магнетронах. Следует, однако, отметить, что магнетрон имеет цилиндрическую, а не плоскую конструкцию электродов и, кроме того, движение электрона в нем сопровождается увеличением или уменьшением энергии. Это обстоятельство мы рассмотрим при изучении магнетронов. Здесь же, анализируя движение электрона в скрещенных радиальном электрическом и аксиальном магнитном полях, будем считать, что 
и электрон перемещается по эпициклоиде (см. рис. 14).
На рис. 15 изображены траектории электрона для Н =const и различных значений напряженности поля Е между анодом и катодом. При r а – r к = const и U K = 0 они соответствуют различным величинам U а.
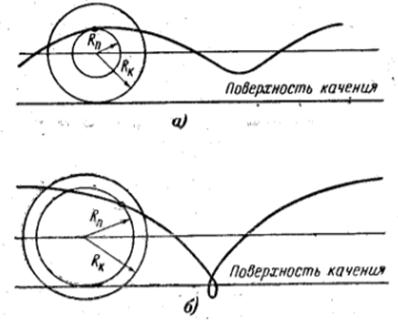
Рис. 14. Траектории движения электрона по укороченной (а) и удлиненной (б) циклоидам.
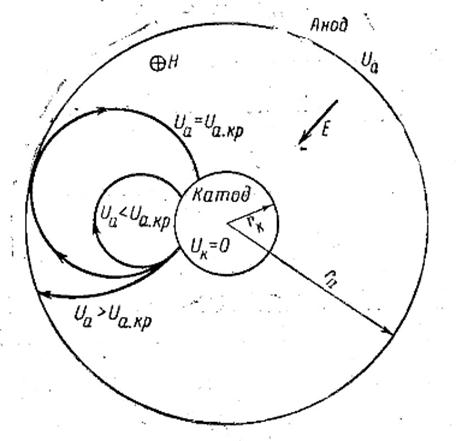
Рис. 15. Траектории электрона в цилиндрическом диоде, помещенном в магнитное поле, при различных значениях U а.
Когда U а мало, электрон, двигаясь по витку эпициклоиды, возвращается на катод. Увеличение потенциала анода сопровождается возрастанием радиуса R K, и при некотором значении U а= U а.кр. максимальное удаление электрона от катода приближенно равно разности радиусов анода и катода r а – r к.
Рис. 16. Парабола критического режима.
Потенциал, при котором электрон лишь касается поверхности анода, называется критическим анодным потенциалом U а.кр.. При U а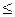 
U а.кр. электроны не достигают анода, а если U а> U а.кр., то все электроны попадают на анод. Значение U а.кр. для плоских электродов можно определить из отношения (40). Для них
, 
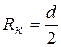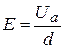
и, следовательно,
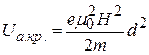. (40)
Для цилиндрических электродов
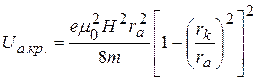. (41)
Зависимость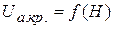 
, представленная на рис. 16, называется параболой критического режима.
