Пример 1. Решите систему уравнений 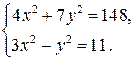
Решение. Решим данную систему уравнений методом подстановки. Из второго уравнения находим: 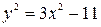 . Подставляя это значение в первое уравнение, получаем:
. Подставляя это значение в первое уравнение, получаем: 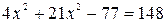 или после упрощения
или после упрощения 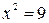 . Корнями этого уравнения являются числа
. Корнями этого уравнения являются числа 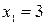 ,
, 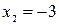 . Таким образом, получаем совокупность двух систем уравнений:
. Таким образом, получаем совокупность двух систем уравнений: 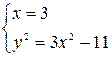 и
и 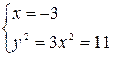 .
.
Первая система имеет решения 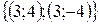 , а вторая
, а вторая 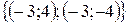 . Значит, данная система имеет решения:
. Значит, данная система имеет решения: 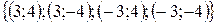 .
.
Ответ. 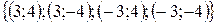 .
.
Пример 2. Решите систему уравнений 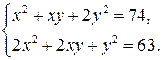
Решение. Метод подстановки в данном случае приводит к сложным выкладкам. Поэтому будем рассуждать иначе: прибавим к первому уравнению системы второе уравнение, тогда получаем систему: 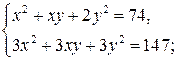
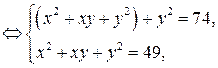 равносильную заданной.
равносильную заданной.
А теперь воспользуемся методом подстановки:
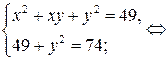
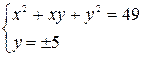 .
.
Полученная система уравнений равносильна совокупности двух систем уравнений:
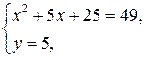 ,
, 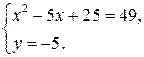
Первая система имеет решение 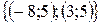 , а вторая
, а вторая 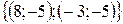 . Значит, решение данной системы имеет вид:
. Значит, решение данной системы имеет вид: 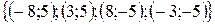 .
.
Ответ. 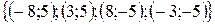 .
.
Пример 3. Решите систему 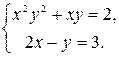
Решение. Обозначим выражение 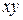 переменной
переменной 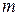 , тогда получим новую систему уравнений
, тогда получим новую систему уравнений 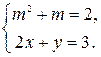
Решая первое уравнение системы, получаем:
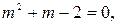
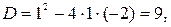 D >0;
D >0;
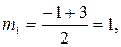
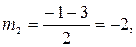
Перейдем к переменным 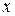 и
и 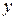 , и решим соответствующие совокупности систем уравнений.
, и решим соответствующие совокупности систем уравнений.
Если 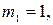 то система примет вид:
то система примет вид:
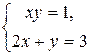 ; тогда
; тогда 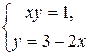 , откуда
, откуда 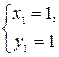 и
и 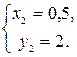
Если 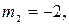 то система примет вид:
то система примет вид:
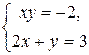 ; тогда
; тогда 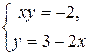 , откуда
, откуда 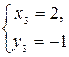 и
и 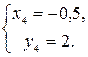
Данная система имеет четыре решения:
(1;1), (0,5;2), (2;-1), (-0,5;4).
Ответ. (1;1), (0,5;2), (2;-1), (-0,5;4).
Пример 4. Решите систему уравнений: 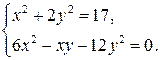
Решение. Второе уравнение системы представим в виде: 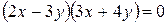 . Тогда данная система будет равносильна совокупности двух систем, решаемых методом подстановки.
. Тогда данная система будет равносильна совокупности двух систем, решаемых методом подстановки.
1. 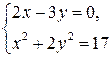 или
или 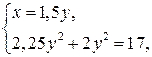 , значит,
, значит, 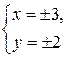 и решением первой системы будет
и решением первой системы будет 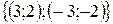 .
.
2. 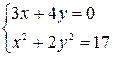 или
или 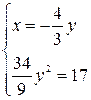
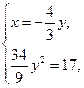 , значит
, значит 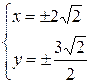 , и решением второй системы будет
, и решением второй системы будет 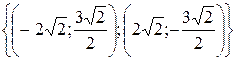 .
.
Ответ. 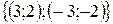 и
и 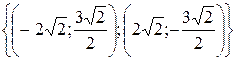 .
.
 2015-04-01
2015-04-01 484
484








