При решении уравнений, содержащих переменную под знаком модуля, применяются чаще всего следующие методы:
1) раскрытие модуля по определению;
2) возведение обеих частей уравнения в квадрат;
3) метод разбиения на промежутки.
При решении неравенства, содержащих переменную под знаком модуля, иногда бывает полезна теорема 1 о равносильности неравенств.
Теорема 1. Пусть дано неравенство 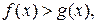 причем
причем 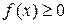 и
и 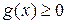 при всех
при всех 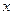 из области определения неравенства. Если обе части возвести в одну и туже натуральную степень
из области определения неравенства. Если обе части возвести в одну и туже натуральную степень 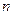 и при этом знак неравенства оставить без изменения, то получится неравенство
и при этом знак неравенства оставить без изменения, то получится неравенство 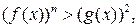 равносильное данному.
равносильное данному.
Пусть, например, нужно решить неравенство 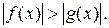 Воспользуемся тем, что если
Воспользуемся тем, что если 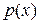 - некоторая функция, то
- некоторая функция, то 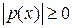 и
и 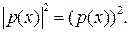
Это значит. что по теореме 1 неравенство 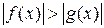 равносильно неравенству
равносильно неравенству 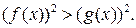 Кроме того, иногда полезно воспользоваться геометрической интерпретацией модуля действительного числа. Дело в том, что геометрически
Кроме того, иногда полезно воспользоваться геометрической интерпретацией модуля действительного числа. Дело в том, что геометрически 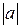 означает расстояние от точки
означает расстояние от точки 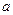 числовой координат, а
числовой координат, а 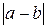 расстояние между точками
расстояние между точками 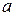 и
и 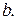
 2015-04-01
2015-04-01 296
296








