2015-04-01
411
Таблица чисел, содержащая m строк и n столбцов вида
,
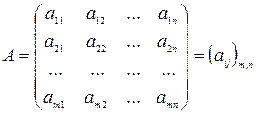называется матрицей порядка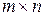 
. Матрица порядка 
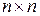называется квадратной матрицей порядка п (А = 
).
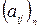Две матрицы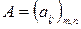 
и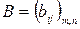 
называются равными 
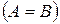, если равны их соответствующие элементы, т.е. 
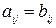(i=1,…,m; j=1,…,n).
Суммой двух матриц 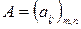и 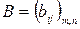одинакового порядка называется матрица 
(
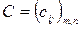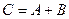), элементы которой определяются равенствами 
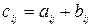(i=1,…,m; j=1,…,n). (1)
Произведением матрицы 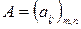на число 
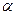называется матрица 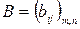(В = 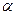А или B = А 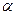), элементы которой определяются равенствами 
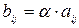(i =1,…,m; j =1,…,n). (2)
Произведением матрицы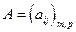 
на матрицу 
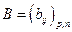называется матрица 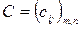(С = AB), элементы которой определяются равенствами
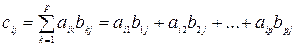
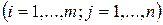. (3)
Заметим, что умножение матрицы А на матрицу В определяется только при условии, что число столбцов матрицы А равно числу строк матрицы В.
Матрица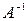 
называется обратной матрицей по отношению к матрице 
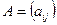, если выполняется условие: 
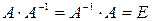, где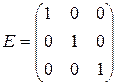 
- единичная матрица.
Дадим определение обратной матрицы для матрицы третьего порядка. Если определитель матрицы А отличен от нуля, то существует единственная обратная матрица 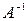, которая находится по формуле:
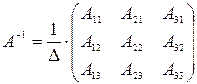, (4)
где ∆ - определитель матрицы А,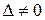 
, 
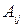- алгебраические дополнения элементов матрицы А.
След матрицы – это сумма элементов главной диагонали матрицы, то есть если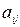 
- элементы матрицы 
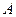, то ее след 
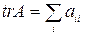. (5)
