Пример 1. В параллелепипеде АВСD 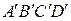 даны координаты вершин А, В, С,
даны координаты вершин А, В, С, 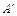 .
. 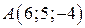 ,
, 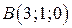 ,
, 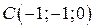 ,
, 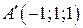 .Найти: 1) координаты вершин D; 2) площадь грани АВСD; 3) объем параллелепипеда; 4) уравнение плоскости
.Найти: 1) координаты вершин D; 2) площадь грани АВСD; 3) объем параллелепипеда; 4) уравнение плоскости 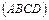 ; 5) уравнение ребра
; 5) уравнение ребра 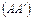 (канонические и общие); 6) угол между диагональю
(канонические и общие); 6) угол между диагональю 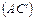 и плоскостью
и плоскостью 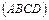 ; 7) уравнение и длину высоты, проведенной из вершины D на грань
; 7) уравнение и длину высоты, проведенной из вершины D на грань 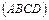 ; 8) координаты точки пересечения высоты Н D’ c гранью
; 8) координаты точки пересечения высоты Н D’ c гранью 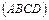 ;
;
Решение. 1. Пусть 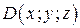 .Воспользовавшись равенством векторов
.Воспользовавшись равенством векторов 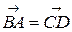 где
где 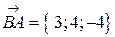 ,
, 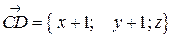 . Получим
. Получим 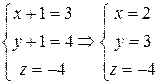 . Координаты точки
. Координаты точки 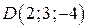 . Ответ:
. Ответ: 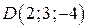 .
.
2. Известно, что 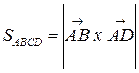 . Находим:
. Находим: 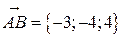 ,
, 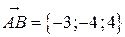 ,
, 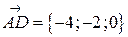 .
.
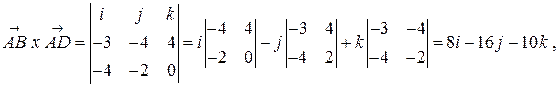
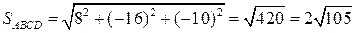 .
.
Ответ: 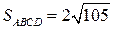 (кв.ед).
(кв.ед).
3. Поскольку 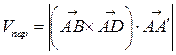 ,
, 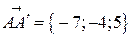 .
.
Находим: 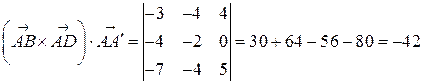 ,
,
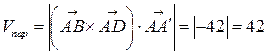 . Ответ:
. Ответ: 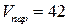 (куб.ед.).
(куб.ед.).
4. Используя формулу 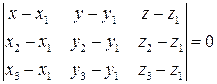 (уравнение плоскости по трем точкам), составляем уравнение плоскости ABCD:
(уравнение плоскости по трем точкам), составляем уравнение плоскости ABCD:
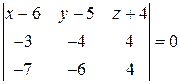 ,
, 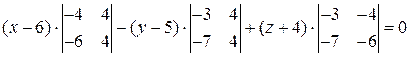
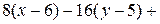
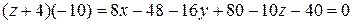

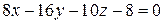
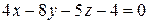 .
.
Ответ: 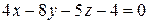 .
.
5. Учитывая уравнение прямой, проходящей через две точки: 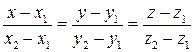 , уравнение прямой
, уравнение прямой  можно записать в виде
можно записать в виде 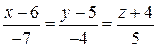 (каноническое уравнение
(каноническое уравнение  ), а общее уравнение ребра
), а общее уравнение ребра  имеет вид:
имеет вид: 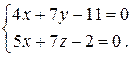
Ответ: 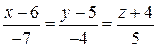
 – каноническое уравнение ребра
– каноническое уравнение ребра 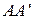 ,
, 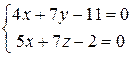 – общее уравнение ребра
– общее уравнение ребра 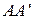 .
.
6. Из равенства 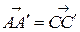 найдем координаты точки
найдем координаты точки 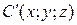
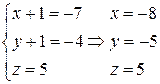 , т.е.
, т.е. 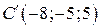 . Тогда
. Тогда 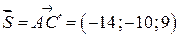 ,
, 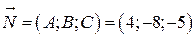 . По формуле
. По формуле
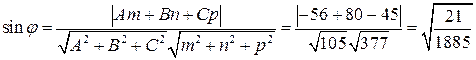 ,
,
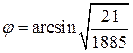 .
.
Ответ: 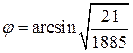 .
.
7. Из условия перпендикулярности прямой 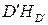 и плоскости АВСD следует, что в качестве направляющего вектора
и плоскости АВСD следует, что в качестве направляющего вектора 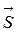 можно взять нормальный вектор
можно взять нормальный вектор 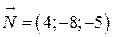 плоскости АВСD. Тогда уравнение прямой
плоскости АВСD. Тогда уравнение прямой 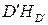 с учетом уравнений
с учетом уравнений 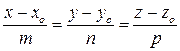 (каноническое уравнение прямой) запишется в виде
(каноническое уравнение прямой) запишется в виде 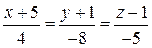 , где координаты точки
, где координаты точки 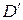 находим: из равенства векторов
находим: из равенства векторов 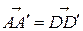 ,
, 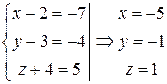 , т.е.
, т.е. 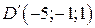 . Длину высоты
. Длину высоты 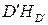 вычисляем как расстояние от точки
вычисляем как расстояние от точки 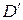 до плоскости АВСD по формуле:
до плоскости АВСD по формуле:
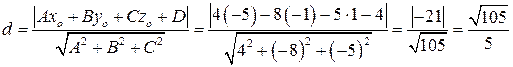 .
.
Ответ: 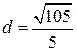 .
.
8. Запишем параметрическое уравнение прямой 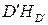 , перпендикулярной к данной плоскости АВСD,
, перпендикулярной к данной плоскости АВСD, 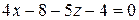 (уравнение плоскости АBCD).
(уравнение плоскости АBCD). 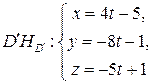 – параметрическое уравнение прямой
– параметрическое уравнение прямой 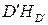 . Решив их совместно с уравнением данной плоскости, найдем параметр t: т.е.
. Решив их совместно с уравнением данной плоскости, найдем параметр t: т.е. 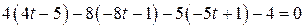 ,
,
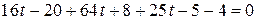 ,
, 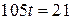 ,
, 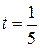 .
.
Следовательно, координаты точки Н пересечения прямой 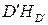 с плоскостью ABCD:
с плоскостью ABCD: 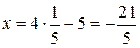 ,
, 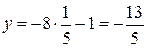 ,
, 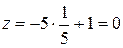 .
.
Итак 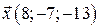 .
.
Ответ. 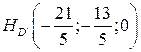 .
.
 2015-04-01
2015-04-01 14264
14264
