Пример 1: Вычислить произведение матриц 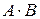 , где
, где
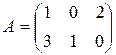 и
и 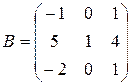 .
.
Решение: Найдем размер матрицы-произведения (если умножение матриц возможно): 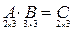 .
.
Вычислим элементы матрицы-произведения, умножая элементы каждой строки первой матрицы на соответствующие элементы столбцов второй матрицы следующим образом:
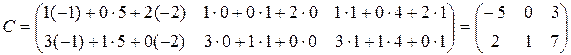 .
.
Ответ: 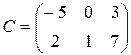 .
.
Пример 2: Найти матрицу Аn и её след: 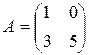 ,
, 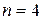 .
.
Решение. Будем находить по порядку все степени матрицы:
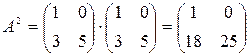 ;
;
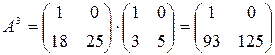 ;
;
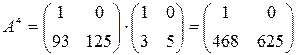 .
.
Найдем след матрицы 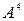 . По определению следа матрицы имеем
. По определению следа матрицы имеем 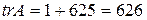 .
.
Ответ: 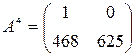 ,
, 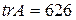 .
.
Пример 3: Найти матрицу, обратную данной: 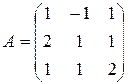 .
.
Решение: Определитель матрицы 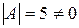 , т.е. обратная матрица
, т.е. обратная матрица 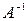 существует.
существует.
Найдем алгебраические дополнения элементов матрицы 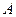 .
.
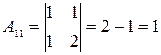 ;
; 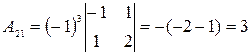 ;
; 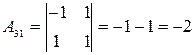 ;
; 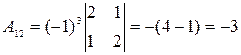 ;
;
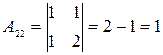 ;
; 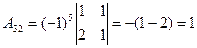 ;
;
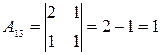 ;
; 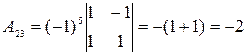 ;
; 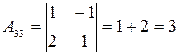 .
.
Используя формулу (4) запишем обратную матрицу 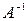 .
.
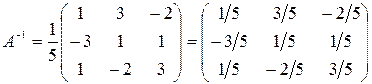 .
.
Ответ: 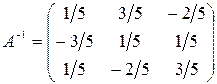 .
.
 2015-04-01
2015-04-01 651
651








