Решение типовых задач. Пример 1. Решить систему методом Гаусса

Пример 1. Решить систему методом Гаусса: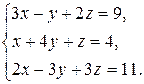

Решение. Метод Гаусса заключается в последовательном исключении неизвестных из уравнений системы. Для удобства его применения поменяем местами 1-е и 2-е уравнения, чтобы в первом уравнении коэффициент при х равнялся единице: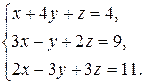

Теперь исключим х из второго и третьего уравнений. Для этого вычтем из второго уравнения первое, умноженное на 3, а из третьего – первое, умноженное на 2: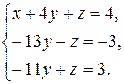

Далее можно легко исключить z из третьего уравнения, если прибавить к нему второе: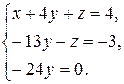

Из последнего уравнения получаем, что у = 0. Подставляя это значение в первое и второе уравнения, находим остальные неизвестные: z = 3, х = 1.

Ответ. х = 1, у = 0, z = 3.

Пример 2. Решить систему уравнений методом Гаусса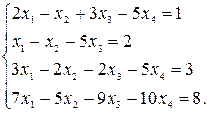

Решение. Для удобства будем работать с расширенной матрицей системы. В результате преобразований над данной матрицей получим:

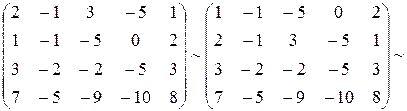
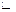
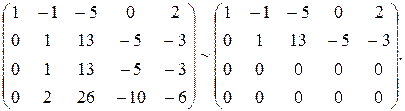
Данная система свелась к ступенчатой

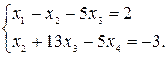
Поэтому общее решение системы имеет вид 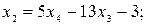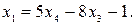Если положить, например, 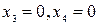, то найдем одно из частных решений этой системы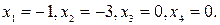

Ответ. Общее решение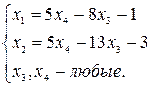

Пример 3. Решить систему уравнений методом Гаусса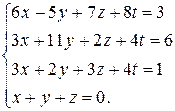

Решение. В результате преобразований над расширенной матрицей системы получим:

.

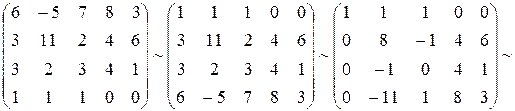
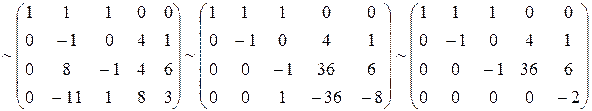Данная система свелась к ступенчатой

.

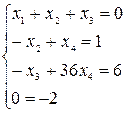Последнее равенство в данной системе - ложное, поэтому данная система решений не имеет.

Ответ. Система не имеет решения.