Пример 1. Доказать, что система векторов 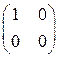 ,
, 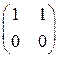 ,
, 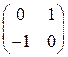
линейного пространства квадратных матриц второго порядка с действительными элементами линейно независима.
Решение. Найдём значения 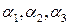 , при которых выполняется равенство
, при которых выполняется равенство 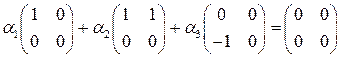 ,
,
или 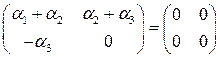
Это равенство равносильно системе уравнений
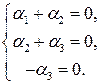
Полученная система уравнений имеет только нулевое решение
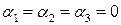 . Следовательно, система векторов линейна независима.
. Следовательно, система векторов линейна независима.
Пример 2. Векторы 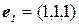 ,
, 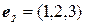 ,
, 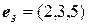 и
и 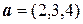 заданы своими координатами в некотором базисе. Показать, что векторы
заданы своими координатами в некотором базисе. Показать, что векторы 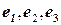 сами образуют базис, и найти координаты вектора
сами образуют базис, и найти координаты вектора 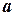 в этом базисе.
в этом базисе.
Решение. Так как каждый из данных векторов имеет три координаты, то эти векторы принадлежат трёхмерному пространству. Для того чтобы три вектора 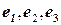 составляли базис трёхмерного пространства достаточно, чтобы они были линейно независимыми. Составим матрицу
составляли базис трёхмерного пространства достаточно, чтобы они были линейно независимыми. Составим матрицу 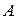 , столбцы которой есть координаты векторов
, столбцы которой есть координаты векторов 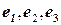 , и найдём её ранг:
, и найдём её ранг:
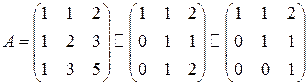
Ранг матрицы 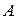 равен 3, следовательно, векторы
равен 3, следовательно, векторы 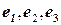 линейно независимы и, значит, составляют базис пространства.
линейно независимы и, значит, составляют базис пространства.
Для нахождения координат 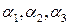 вектора
вектора 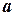 составим и решим векторное уравнение
составим и решим векторное уравнение 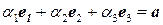 , или
, или
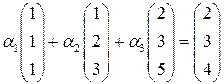 .
.
Это уравнение равносильно системе линейных уравнений с такой расширенной матрицей
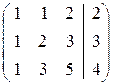 .
.
Используя метод Гаусса, получим 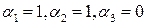 .
.
 2015-04-01
2015-04-01 1973
1973
