Рассмотрим однородную линейную систему
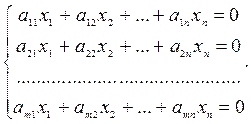 (1.20)
(1.20)
Очевидно, что такая система всегда совместна, поскольку имеет нулевое решение 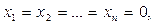 называемое тривиальным.
называемое тривиальным.
Матрицей системы (6) называется матрица вида
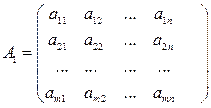 . (2.20)
. (2.20)
Пусть ранг матрицы системы r < n. Неизвестные 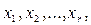 коэффициенты при которых входят в базисный минор матрицы системы, называются базисными неизвестными, а остальные (
коэффициенты при которых входят в базисный минор матрицы системы, называются базисными неизвестными, а остальные (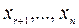 ) – свободными неизвестными.
) – свободными неизвестными.
Тогда число линейно независимых решений системы (1.20) равно n – r. При этом любые n – r линейно независимых решений системы (1.20) называются ее фундаментальной системой решений, а любое решение однородной линейной системы (1.20.) является линейной комбинацией фундаментальной системы ее решений, то есть 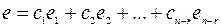 , где
, где 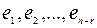 - фундаментальная система решений.
- фундаментальная система решений.
Пример 1.
Найти фундаментальную систему решений однородной линейной системы
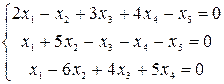 .
.
Решение.
Найдем r (A):
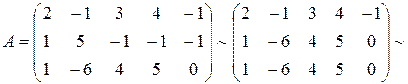
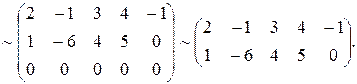
Выберем в качестве базисного минора 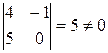 .
.
Значит, r (A) = 2. Пусть х 4, х 5 – базисные неизвестные, х 1, х 2, х 3 – свободные неизвестные. Запишем для них новую систему:
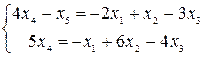 ,
,
откуда 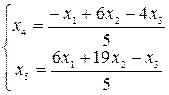 .
.
Фундаментальная система решений состоит из трех векторов. Рассмотрим три набора значений свободных неизвестных:
1) х 1 = 1, х 2 = х 3 = 0.
Тогда х 4 = -0,2, х 5 = 1,2, и решение можно записать в виде строки
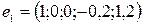 .
.
2) х 1 = 0, х 2 = 1, х 3 = 0.
При этом х 4 = 1,2, х 5 = 3,8, и следующее решение системы имеет вид
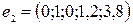 .
.
3) х 1 = х 2 = 0, х 3 = 1. Отсюда х 4 = -0,8, х 5 = -0,2, и последняя строка
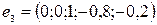 .
.
Фундаментальная система решений, построенная при таком выборе свободных неизвестных, называется нормальной. Поскольку строки свободных неизвестных 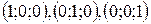 линейно независимы, это гарантирует линейную независимость решений
линейно независимы, это гарантирует линейную независимость решений 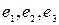 .
.
Итак, в качестве фундаментальной системы решений можно выбрать
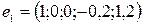 ,
, 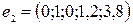 ,
, 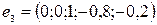 .
.
При этом любое решение данной системы имеет вид: 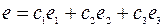 , где с 1, с 2, с 3 – произвольные постоянные. Эта формула задает общее решение системы.
, где с 1, с 2, с 3 – произвольные постоянные. Эта формула задает общее решение системы.
Пример 2. Найти фундаментальную систему решений системы уравнений. 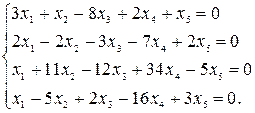
Решение. Выпишем матрицу системы, подставив последнее уравнение на первое место, затем приведем ее к ступенчатому виду:
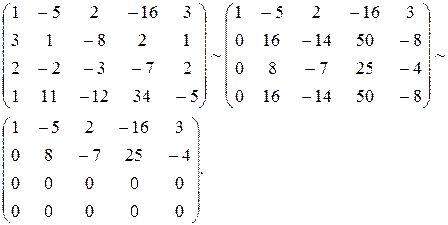
Ранг матрицы 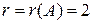 . Базисный минор при переменных
. Базисный минор при переменных 
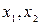
 отличен от нуля:
отличен от нуля: 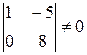 ; выбираем
; выбираем 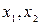 в качестве базисных переменных и выражаем их через свободные
в качестве базисных переменных и выражаем их через свободные 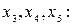
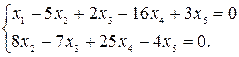
Для получения фундаментальной системы решений 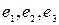 поочередно заменяем неосновные переменные
поочередно заменяем неосновные переменные 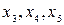 элементами строк единичной матрицы
элементами строк единичной матрицы 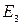 .
.
При 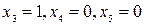 приведенная выше система принимает вид:
приведенная выше система принимает вид:
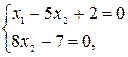 откуда
откуда 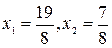 , т.е. получаем базисное решение
, т.е. получаем базисное решение 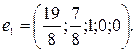
Аналогично находим еще два базисных решения:
при 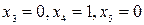
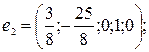
при 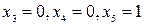
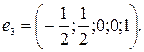
Найденные решения (векторы) 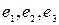 образуют фундаментальную систему. Умножив компоненты решения
образуют фундаментальную систему. Умножив компоненты решения 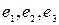 соответственно на 8, 8, 2, получим фундаментальную систему решений с целыми компонентами.
соответственно на 8, 8, 2, получим фундаментальную систему решений с целыми компонентами.
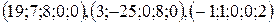 .
.
 2015-04-01
2015-04-01 484
484








