19.1. Проверить, что векторы 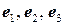 образуют базис трехмерного пространства; найти координаты вектора
образуют базис трехмерного пространства; найти координаты вектора 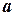 в этом базисе:
в этом базисе:
а) 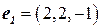 ,
, 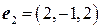 ,
, 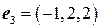 ,
, 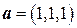 .
.
б) 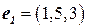 ,
, 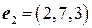 ,
, 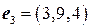 ,
, 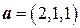 .
.
19.2. Доказать, что матрицы 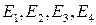 образуют базис пространства квадратных матриц второго порядка с действительными элементами, и найти координаты матрицы
образуют базис пространства квадратных матриц второго порядка с действительными элементами, и найти координаты матрицы 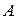 в этом базисе.
в этом базисе.
а) 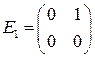 ,
, 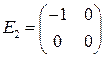 ,
, 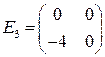 ,
, 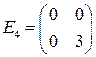 ;
; 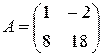 .
.
б) 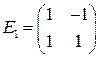 ,
, 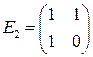 ,
, 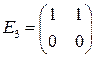 ,
, 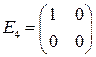 ;
; 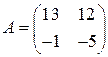 .
.
19.3. Исследовать на линейную зависимость систему векторов 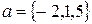 ,
, 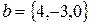 ,
, 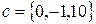 .
.
19.4. Доказать, что векторы 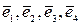 образуют базис векторного пространства
образуют базис векторного пространства 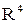 . Разложить вектор
. Разложить вектор 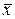 по этому базису, если
по этому базису, если 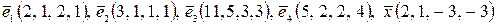 .
.
Домашнее задание
19.5. Доказать, что система векторов линейно зависима 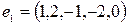 ,
, 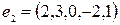 ,
, 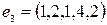 ,
, 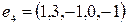 .
.
19.6. Доказать, что векторы 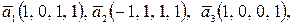
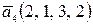 образуют базис в
образуют базис в 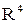 (если известно, что размерность
(если известно, что размерность 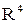 равна четырем) и разложить вектор
равна четырем) и разложить вектор 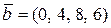 по этому базису.
по этому базису.
Ответы
19.1. а) 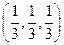 , б) (0, -5, 4). 19.2. а) (-2, -1, -2, 6), б) (-5, 4, 3, 11). 19.3. система линейно зависима. 19.4.
, б) (0, -5, 4). 19.2. а) (-2, -1, -2, 6), б) (-5, 4, 3, 11). 19.3. система линейно зависима. 19.4. 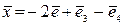 . 19.6.
. 19.6. 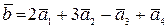
 2015-04-01
2015-04-01 1122
1122
