Пример 1. Найти производную третьего порядка функции 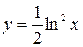 .
.
Решение. Сначала найдем 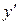 и
и 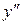 , обязательно упрощая полученные выражения
, обязательно упрощая полученные выражения
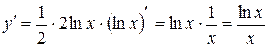 ;
;
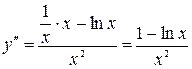 ;
;
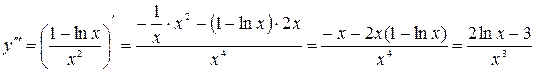 .
.
Ответ. 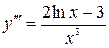 .
.
Пример 2. Найти производную 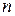 -го порядка функции
-го порядка функции 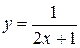 .
.
Решение. Преобразуем исходную функцию следующим образом 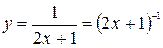 .
.
Вычислим производные функции.
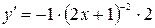 ;
;
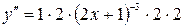 ;
;
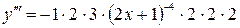 ;
;
…
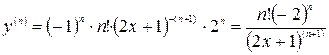 .
.
Ответ. 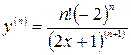 .
.
Пример 3. Разложить в степенной ряд функцию 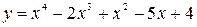 по степеням
по степеням 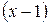 .
.
Решение. Для разложения функции воспользуемся формулой Тейлора (1). Вычислим сначала все производные функции и значения этих производных в точке 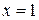 .
.
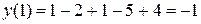 ;
;
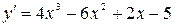 ;
; 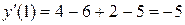 ;
;
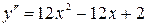 ;
; 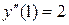 ;
;
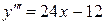 ;
; 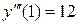 ;
;
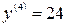 ;
;
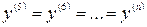 .
.
Подставляя получившиеся значения в формулу Тейлора, получим разложение исходной функции в степенной ряд:
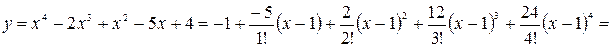
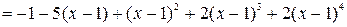 .
.
Ответ. 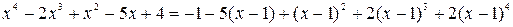 .
.
 2015-04-01
2015-04-01 360
360








