Краткие теоретические сведения. Определение. Функция называется возрастающей (убывающей) в промежутке из области определения, если для любых из условия

Определение. Функция называется возрастающей (убывающей) в промежутке 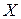из области определения, если для любых 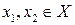из условия 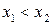следует неравенство 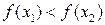(соответственно ).

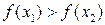Под монотонностью понимается либо возрастание, либо убывание.

Теорема (достаточное условие монотонности). Если функция дифференцируема в промежутке и 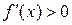(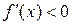) для всех 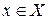, то возрастает (соответственно убывает) в промежутке .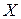

Определение. Точка называется точкой минимума (максимума) функции 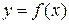, если она определена в некоторой окрестности этой точки и для каждой точки 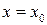этой окрестности 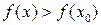(соответственно 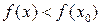). Значение функции 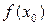называется минимумом (соответственно максимумом).

Под экстремумом функции (локальным) понимается либо минимум функции, либо её максимум.

Определение. Точка из области определения функции 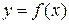, называется стационарной точкой, если дифференцируема в и .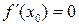

Определение. Точка из области определения функции 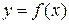, называется критической точкой, если не дифференцируема в .

Необходимое условие экстремума. Если - точка экстремума функции , то она является стационарной ил критической точкой этой функции.

Не всякая критическая или стационарная точка является точкой экстремума.

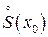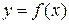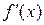Первое достаточное условие экстремума. непрерывна в точке и дифференцируема в . Пусть - стационарная или критическая точка функции . Если в некоторой окрестности точки слева от производная принимает один знак, а справа от - противоположный, то - точка экстремума. При этом если слева 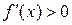, справа 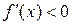, то - точка максимума, в противном случае - точка минимума. Если в некоторой проколотой окрестности точки производная 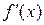имеет постоянный знак, то не является точкой экстремума. Если к тому же непрерывна в , то функция монотонна в этой окрестности.

Второе достаточное условие экстремума. Пусть 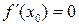и существует 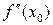. Тогда если 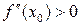, то - точка минимума. Если же 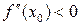, то - точка максимума.

Вторым достаточным условием экстремума удобно пользоваться, если достаточно сложно установить знак первой производной в окрестности точки экстремума.

Пусть функция 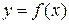имеет конечную или бесконечную производную в каждой точке интервала 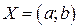. Обозначим 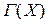дугу графика функции , соответствующую интервалу .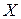

Определение. Если дуга 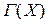лежит не ниже (не выше) касательной к графику функции 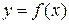, проведенной в любой точке 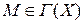, то функция называется выпуклой (соответственно вогнутой) в интервале .

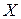Точка на графике функции, в которой существует касательная к графику функции, называется точкой перегиба функции или графика функции, если она является границей дуг графика с разными направлениями выпуклости (рис. 24.1 б, в).

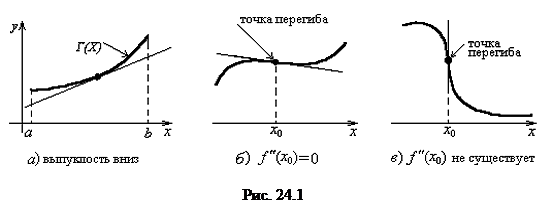
Заметим, что в точке перегиба требуется существование касательной к графику.

Теорема (достаточное условие выпуклости вверх и вниз). Если функция дифференцируема дважды в интервале 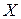и в нём 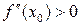(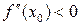), то является выпуклой вниз (соответственно выпуклой вверх) в интервале .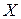

Необходимое условие точки перегиба. Если 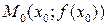- точка перегиба функции , то либо 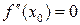, либо 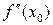не существует (рис. 24.1 б, в). Следовательно, абсциссы точек перегиба нужно искать в тех значениях x, при которых вторая производная либо равна нулю, либо не существует.

Достаточное условие точки перегиба. Пусть функция имеет производную (может быть бесконечную) в точке , существует вторая производная в проколотой окрестности точки и либо 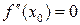, либо 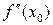не существует. Тогда если при переходе через 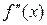меняет знак, то 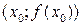является точкой перегиба.