2015-04-01
628
При решении задач на определение экстремумов функции одного переменного придерживаются следующей схемы:
1) Установить область определения функции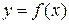 
.
2) Найти ее первую производную.
3) Найти стационарные и критические точки.
4) Применить к каждой точке достаточное условие существования экстремума для решения вопроса о его наличии.
Пример 1. Исследовать функцию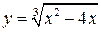 
на экстремум и монотонность.
Решение. Область определения – множество всех действительных чисел.
1) Находим производную функции:
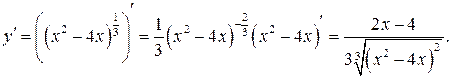
2) Найдем стационарные и критические точки. Решим уравнение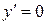 
: 
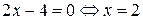- стационарная; 
не существует при 
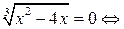
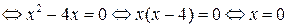или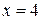 
. Эти точки входят в область определения функции, следовательно, являются критическими.
3) Разобьем область определения 
точками 0, 2, 4 на интервалы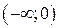 
, 
, 
, 
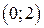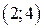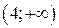, в каждом из которых производная сохраняет знак. Найдем знаки производной в этих интервалах.
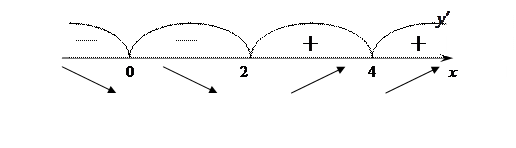
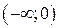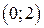4) Функция убывает в интервалах и , возрастает в интервалах 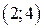и 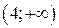. Однако можно сделать более сильный вывод. В самом деле, в окрестностях критических точек 
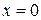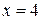и производная не меняет знака, значит, они не являются точками экстремума. Функция убывает в интервале 
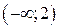и возрастает в интервале 
.
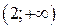5) Стационарная точка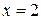 
является точкой минимума. Тогда 
.
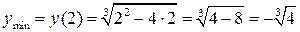Пример 2. Найти экстремумы функции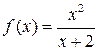 
.
Решение. Данная функция определена для всех действительных чисел, кроме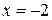 
. Дифференцируя частное, получим
.
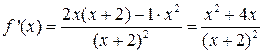Очевидно, что производная также определена при всех x, кроме 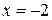. Из уравнения 
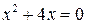находим стационарные точки: 
, 
.
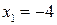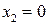Разобьем область определения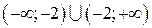 
точкам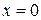и и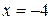 
на интервалы 
, 
, 
, 
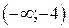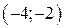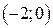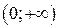, в каждой из которых производная сохраняет знак. Найдем знаки производной в этих интервалах.
 |
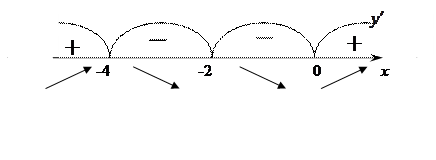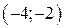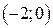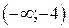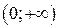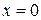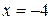Функция убывает в интервалах и , возрастает в интервалах и . Кроме того, в окрестностях стационарных точек и производная меняет знак, значит, они являются точками экстремума) Таким образом, 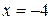– точка максимума и 
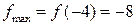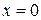, – точка минимума (
).
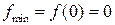При исследовании функции на выпуклость и вогнутость функции придерживаются следующей схемы:
1) Установить область определения функции .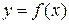
2) Найти вторую производную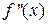 
.
3) Выяснить, в каких точках из области определения вторая производная обращается в нуль (т.е. решить уравнение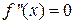 
) или не существует.
4) Установить знак второй производной на числовых интервалах, на которые найденные точки разбили область определения, и определить направления выпуклости (если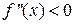 
, то график функции направлен выпуклостью вверх, т.е. Ç; если 
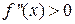– выпуклостью вниз, т.е. È).
5) Если при переходе через найденную точку 
направление выпуклости меняется и существует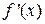 
, то точка 
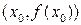– точка перегиба графика функции.
Пример 3. Исследовать функцию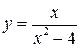 
на выпуклость, вогнутость, найти точки перегиба.
Решение. 1) Функция определена при всех действительных значениях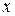 
, таких, что 
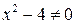, т.е. 
.
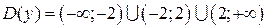2) Найдем вторую производную.
,
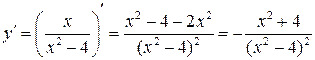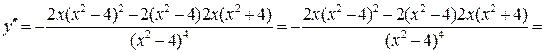
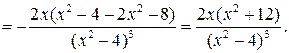
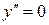при . 
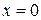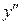не существует при 
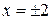, но эти точки не входят в область определения функции, поэтому они не могут быть абсциссами точек перегиба.
3) Разобьем область определения точкой 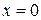на интервалы 
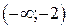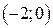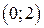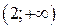, , , , в каждом из которых вторая производная сохраняет знак.
Определим знак второй производной в каждом из этих интервалов.
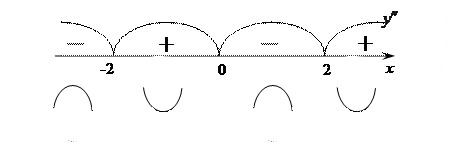
4) Функция выпукла вверх в интервалах 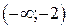, 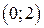; выпукла вниз в интервалах , .
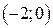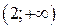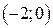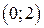
5) В интервалах , 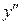имеет разные знаки. Значит, точка 
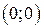является точкой перегиба графика функции.
