Краткие теоретические сведения. Не для всякой иррациональной функции можно найти первообразную в виде элементарной функции

Не для всякой иррациональной функции можно найти первообразную в виде элементарной функции. Рассмотрим интегралы от некоторых иррациональных функций, которые с помощью определённых подстановок приводятся к интегралам от рациональных функций новой переменной.

I. Интеграл вида 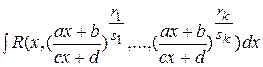, где 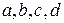– постоянные, 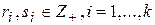приводятся к интегралу от рациональной функции новой переменной 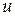с помощью подстановки 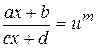, где 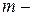наименьшее общее кратное (НОК) знаменателей дробей 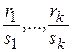, т.е. .

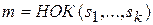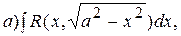
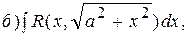
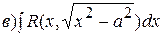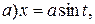
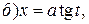
II. Интегралы вида тригонометрическими подстановками соответственно 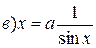сводятся к уже рассмотренным интегралам вида .

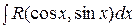К рассмотренным интегралам могут быть преобразованы интегралы 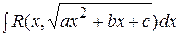, если из квадратного трёхчлена выделить полный квадрат суммы и сделать линейную замену переменной. Существуют и другие методы интегрирования указанного интеграла, мы их здесь не рассматриваем.