I. Интегралы вида 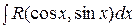 приводятся к интегралам от рациональной функции новой переменной
приводятся к интегралам от рациональной функции новой переменной 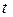 с помощью универсальной тригонометрической подстановки
с помощью универсальной тригонометрической подстановки 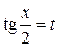 . В этом случае
. В этом случае 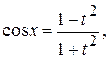
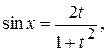
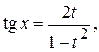
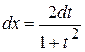 .
.
Подставляя в подынтегральное выражение вместо 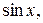
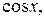
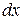 их выражения через
их выражения через 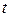 ,
, 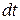 , получим интеграл от рациональной дроби:
, получим интеграл от рациональной дроби:
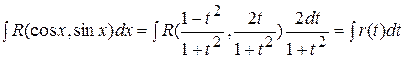 .
.
В случае, когда имеет место тождество  , для приведения подынтегральной функции к рациональному виду можно применять упрощённую подстановку
, для приведения подынтегральной функции к рациональному виду можно применять упрощённую подстановку 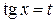 . При этом
. При этом  .
.
Если 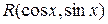 – нечётная функция относительно
– нечётная функция относительно 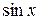 , т.е.
, т.е. 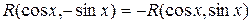 , то интеграл рационализируется подстановкой
, то интеграл рационализируется подстановкой 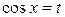 .
.
Если 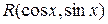 – нечётная функция относительно
– нечётная функция относительно 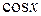 , т.е.
, т.е. 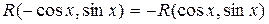 , то интеграл рационализируется подстановкой
, то интеграл рационализируется подстановкой 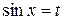 .
.
II. Для отыскания интегралов вида 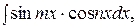
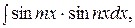
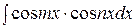 используют следующие формулы:
используют следующие формулы:
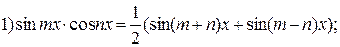
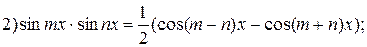
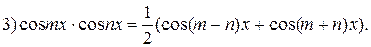
При нахождении интегралов вида 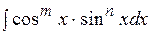
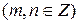 возможны следующие случаи:
возможны следующие случаи:
1) хотя бы одно из чисел 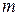 или
или 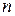 – нечётное, например
– нечётное, например 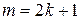 , тогда
, тогда 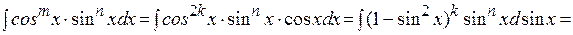
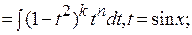
2) оба числа 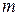 и
и 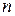 – чётные, тогда рекомендуется использовать следующие формулы, позволяющие понизить степень тригонометрических функций:
– чётные, тогда рекомендуется использовать следующие формулы, позволяющие понизить степень тригонометрических функций: 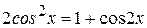 ,
, 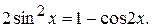
 2015-04-01
2015-04-01 515
515








