Пусть на отрезке 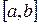 задана функция
задана функция  . Выполним следующие операции:
. Выполним следующие операции:
1. С помощью точек деления 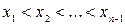 разобьем
разобьем 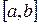 на
на 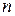 малых отрезков:
малых отрезков: 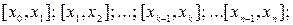
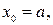
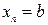 .
.
2. На каждом малом отрезке выберем произвольную точку 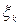 ,
, 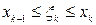 , составим произведение
, составим произведение 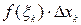 .
.
3. Составим, так называемую, интегральную сумму всех таких произведений
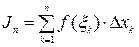 .
.
Определенный интеграл есть число, равное пределу, к которому стремится интегральная сумма 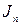 , когда
, когда 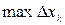 стремится к нулю.
стремится к нулю.
Таким образом, 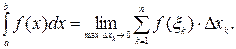
Числа а и b называются соответственно нижним и верхним пределами (границами) интегрирования,  - подынтегральной функцией, а интервал
- подынтегральной функцией, а интервал 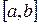 - областью интегрирования.
- областью интегрирования.
Функция  , для которой существует конечный
, для которой существует конечный 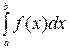 , называется интегрируемой на промежутке
, называется интегрируемой на промежутке 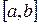 , причем указанный предел не зависит ни от способа разбиения сегмента
, причем указанный предел не зависит ни от способа разбиения сегмента 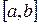 на части, ни от выбора точек
на части, ни от выбора точек 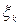 в каждой из них.
в каждой из них.
Свойства определенных интегралов.
1. 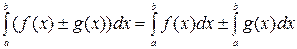 .
.
2. 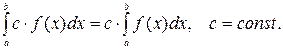
3. 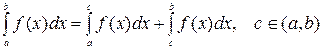 .
.
4. Если 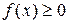 на
на 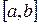 , то
, то 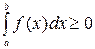 .
.
5. Если 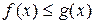 для
для 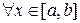 , то
, то
а) 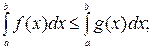
б) 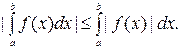
6. Теорема о среднем: 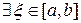 ,
,
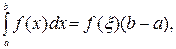 где
где  - непрерывна на [a,b].
- непрерывна на [a,b].
7. 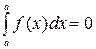 .
.
8. 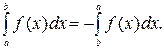
Теорема Ньютона-Лейбница
Пусть  непрерывна на отрезке
непрерывна на отрезке 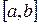 и
и 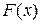 - одна из ее первообразных, тогда справедлива формула
- одна из ее первообразных, тогда справедлива формула
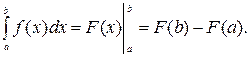
 2015-04-01
2015-04-01 384
384








