Пример 1. Вычислить 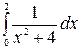 .
.
Решение. Используя формулу Ньютона-Лейбница, а также табличный интеграл, получим
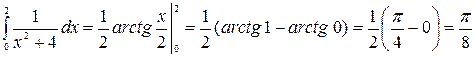 .
.
Ответ. 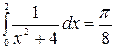 .
.
Пример 2. Вычислить 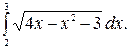
Решение. Преобразуем подкоренное выражение, выделив полный квадрат
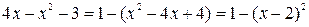 .
.
Введем новую переменную: 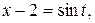 тогда
тогда 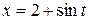 ,
,
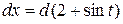 или
или 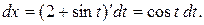
Найдем пределы интегрирования новой переменной t:
если 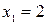 , то
, то 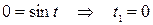
если 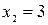 , то
, то 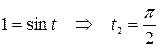 .
.
Воспользуемся формулой замены переменной в определенном интеграле, получим
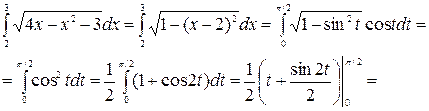
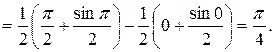
Заметим, что в данном случае при применении формулы замены переменной отпадает необходимость возвращения к старой переменной х по сравнению с неопределенным интегралом. Это вполне объяснимо, ибо определенный интеграл есть некоторое постоянное число, в то время как неопределенный интеграл от той же самой функции есть некоторая функция.
Ответ. 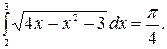
Пример 3. Вычислить 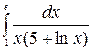 .
.
Решение. Пусть 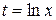 , тогда
, тогда 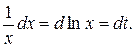
Если 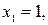 то
то 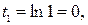 если
если 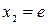 , то
, то 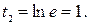
Следовательно,
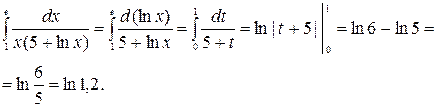
Ответ. 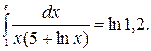
 2015-04-01
2015-04-01 484
484








