Индивидуальные газы, находящиеся в термодинамическом равновесии, характеризуются определенными физическими величинами – равновесными параметрами состояния.
В термодинамике существует подразделение равновесных параметров на термические (давление, температура, объем, термические коэффициенты) и калорические параметры (внутренняя энергия, энтальпия, энтропия, удельная теплоемкость и т.д.).
Для выражения значений термодинамических величин различают: удельные величины, отнесенные к 1 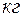 вещества; объемные величины, отнесенные к 1
вещества; объемные величины, отнесенные к 1 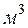 вещества; молярные величины, отнесенные к 1
вещества; молярные величины, отнесенные к 1 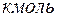 вещества.
вещества.
Из многочисленных термодинамических величин для решения большинства задач при тепловых расчетах достаточно ограничится следующими термодинамическими и калорическими параметрами:
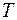 – термодинамическая температура в
– термодинамическая температура в 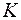 ;
;
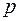 – абсолютное давление в
– абсолютное давление в 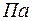 ;
;
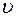 - удельный объем в
- удельный объем в 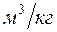 ;
;
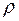 - плотность в
- плотность в 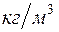 ;
; 
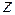 - фактор сжимаемости;
- фактор сжимаемости;
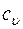 - удельная изохорная теплоемкость в
- удельная изохорная теплоемкость в 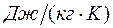 ;
;
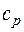 - удельная изобарная теплоемкость в
- удельная изобарная теплоемкость в 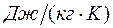 ;
;
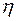 - динамический коэффициент вязкости в
- динамический коэффициент вязкости в 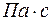 ;
;
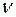 - кинематический коэффициент вязкости в
- кинематический коэффициент вязкости в 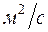 ;
;
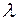 - коэффициент теплопроводности в
- коэффициент теплопроводности в 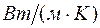 ;
;
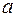 - коэффициент температуропроводности в
- коэффициент температуропроводности в 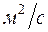 ;
;
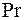 - число Прандтля;
- число Прандтля;
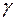 - показатель адиабаты;
- показатель адиабаты;
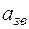 - скорость звука в газе в
- скорость звука в газе в 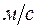 .
.
Термические параметры – температура 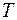 и давление
и давление 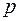 обычно принимаются в качестве задаваемых при проведении расчетов, а остальные параметры – в качестве определяемых теплофизических характеристик конкретного газа.
обычно принимаются в качестве задаваемых при проведении расчетов, а остальные параметры – в качестве определяемых теплофизических характеристик конкретного газа.
Для описания 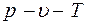 - свойств реальных газов предложено много модификаций уравнения состояния идеального газа. Наиболее важным из известных уравнений, имеющим строгое теоретическое обоснование связи с межмолекулярными силами, является вириальное уравнение состояния. Это уравнение выражает отклонения от уравнения состояния идеального газа в виде степенного ряда по плотности
- свойств реальных газов предложено много модификаций уравнения состояния идеального газа. Наиболее важным из известных уравнений, имеющим строгое теоретическое обоснование связи с межмолекулярными силами, является вириальное уравнение состояния. Это уравнение выражает отклонения от уравнения состояния идеального газа в виде степенного ряда по плотности 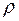 [16].
[16].
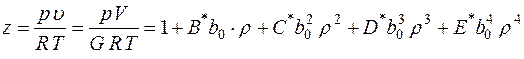 , (1)
, (1)
где 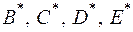 - второй, третий, четвертый и пятый приведенные
- второй, третий, четвертый и пятый приведенные
вириальные коэффициенты соответственно;
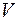 - объем, занимаемый газом, в
- объем, занимаемый газом, в 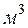 ;
;
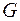 - масса газа в
- масса газа в 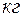 .
.
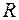 - газовая постоянная в
- газовая постоянная в 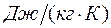 .
.
Вириальные коэффициенты зависят от температуры и природы рассматриваемого газа, причем каждый вириальный коэффициент можно вполне интерпретировать на основании молекулярных свойств. Так второй вириальный коэффициент учитывает отклонения от уравнения состояния идеального газа, обусловленные взаимодействием двух молекул, третий – взаимодействием трех молекул и т. д.
В справочнике [17] приведены таблицы теплофизических свойств (термические и калорические параметры) наиболее важных одно-, двух- и многоатомных газов, рассчитанных по соответствующим уравнениям с использованием уравнения состояния (1).
Формулы взаимосвязи некоторых теплофизических характеристик:
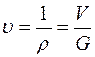
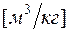 ;
;
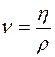
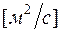 ;
;
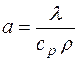
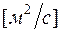 ;
;
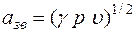
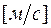 ;
;
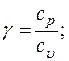
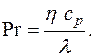
 2015-04-01
2015-04-01 2831
2831
